| The SHEWHART Procedure |
Constructing Charts for Nonconformities per Unit (u Charts)
The following notation is used in this section:
|
expected number of nonconformities per unit produced by process |
||||
|
number of nonconformities per unit in the |
||||
|
total number of nonconformities in the |
||||
|
number of inspection units in the |
||||
|
average number of nonconformities per unit taken across subgroups. The quantity
|
||||
|
number of subgroups |
||||
|
has a central |
Plotted Points
Each point on a  chart indicates the number of nonconformities per unit (
chart indicates the number of nonconformities per unit (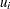 ) in a subgroup. For example, Figure 13.30.12 displays three sections of pipeline that are inspected for defective welds (indicated by an X). Each section represents a subgroup composed of a number of inspection units, which are 1000-foot-long sections. The number of units in the
) in a subgroup. For example, Figure 13.30.12 displays three sections of pipeline that are inspected for defective welds (indicated by an X). Each section represents a subgroup composed of a number of inspection units, which are 1000-foot-long sections. The number of units in the 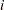 th subgroup is denoted by
th subgroup is denoted by 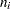 , which is the subgroup sample size.
, which is the subgroup sample size.
 Charts and
Charts and  Charts
Charts
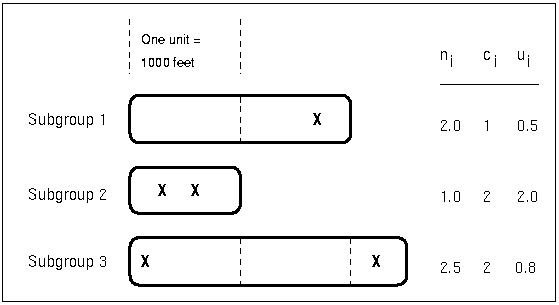
The number of nonconformities in the 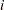 th subgroup is denoted by
th subgroup is denoted by 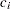 . The number of nonconformities per unit in the
. The number of nonconformities per unit in the 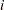 th subgroup is denoted by
th subgroup is denoted by 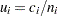 . In Figure 13.30.12, the number of defective welds per unit in the third subgroup is
. In Figure 13.30.12, the number of defective welds per unit in the third subgroup is 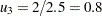 .
.
A  chart plots the quantity
chart plots the quantity 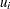 for the
for the  th subgroup. A
th subgroup. A  chart plots the quantity
chart plots the quantity 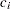 for the
for the 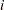 th subgroup (see CCHART Statement). An advantage of a
th subgroup (see CCHART Statement). An advantage of a  chart is that the value of the central line at the
chart is that the value of the central line at the 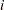 th subgroup does not depend on
th subgroup does not depend on 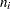 . This is not the case for a
. This is not the case for a  chart, and consequently, a
chart, and consequently, a  chart is often preferred when the number of units
chart is often preferred when the number of units 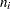 is not constant across subgroups.
is not constant across subgroups.
Central Line
On a  chart, the central line indicates an estimate of
chart, the central line indicates an estimate of  , which is computed as
, which is computed as  by default. If you specify a known value (
by default. If you specify a known value (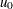 ) for
) for  , the central line indicates the value of
, the central line indicates the value of 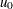 .
.
Control Limits
You can compute the limits in the following ways:
as a specified multiple (
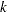 ) of the standard error of
) of the standard error of 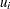 above and below the central line. The default limits are computed with
above and below the central line. The default limits are computed with 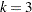 (these are referred to as
(these are referred to as 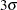 limits).
limits). as probability limits defined in terms of
 , a specified probability that
, a specified probability that 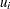 exceeds the limits
exceeds the limits
The lower and upper control limits, LCLU and UCLU, respectively, are given by
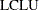 |
 |
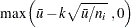 |
|||
 |
 |
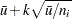 |
The limits vary with 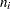 .
.
The upper probability limit UCLU for 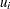 can be determined using the fact that
can be determined using the fact that
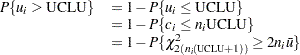 |
The limit UCLU is then calculated by setting
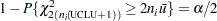 |
and solving for UCLU.
Likewise, the lower probability limit LCLC for 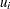 can be determined using the fact that
can be determined using the fact that
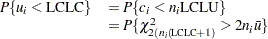 |
The limit LCLC is then calculated by setting
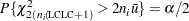 |
and solving for LCLC. For more information, refer to Johnson, Kotz, and Kemp (1992). This assumes that the process is in statistical control and that 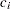 has a Poisson distribution. Note that the probability limits vary with
has a Poisson distribution. Note that the probability limits vary with 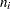 and are asymmetric around the central line. If a standard value
and are asymmetric around the central line. If a standard value 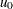 is available for
is available for  , replace
, replace  with
with 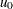 in the formulas for the control limits.
in the formulas for the control limits.
You can specify parameters for the limits as follows:
Specify
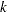 with the SIGMAS= option or with the variable _SIGMAS_ in a LIMITS= data set.
with the SIGMAS= option or with the variable _SIGMAS_ in a LIMITS= data set. Specify
 with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set.
with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set. Specify a constant nominal sample size
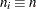 for the control limits with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set.
for the control limits with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set. Specify
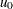 with the U0= option or with the variable _U_ in a LIMITS= data set.
with the U0= option or with the variable _U_ in a LIMITS= data set.
Copyright © SAS Institute, Inc. All Rights Reserved.
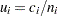 .
. 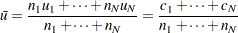
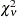
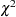 distribution with
distribution with  degrees of freedom
degrees of freedom