| The SHEWHART Procedure |
Example 13.30 Computing Average Run Lengths for s Charts
[See SHWSARL in the SAS/QC Sample Library]This example illustrates how you can compute the average run length of an  chart. The data used here are the power measurements in the data set Turbine, which is introduced in Creating Standard Deviation Charts from Raw Data.
chart. The data used here are the power measurements in the data set Turbine, which is introduced in Creating Standard Deviation Charts from Raw Data.
The in-control average run length of a Shewhart chart is 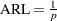 , where
, where 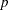 is the probability that a single point exceeds its control limits. Since this probability is saved as the value of the variable _ALPHA_ in an OUTLIMITS= data set, you can compute ARL for an
is the probability that a single point exceeds its control limits. Since this probability is saved as the value of the variable _ALPHA_ in an OUTLIMITS= data set, you can compute ARL for an  chart as follows:
chart as follows:
title 'Average In-Control Run Length'; proc shewhart data=Turbine; schart KWatts*Day / outlimits=Turblim nochart; data ARLcomp; keep _var_ _sigmas_ _alpha_ arl; set Turblim; arl = 1 / _alpha_; run;
The data set ARLcomp is listed in Output 13.30.1, which shows that the ARL is equal to 358.
To compute out-of-control average run lengths, define  as the slippage factor for the process standard deviation
as the slippage factor for the process standard deviation  , where
, where 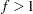 . In other words, the "shifted" standard deviation to be detected by the chart is
. In other words, the "shifted" standard deviation to be detected by the chart is  . The following statements compute the ARL as a function of
. The following statements compute the ARL as a function of  :
:
data ARLshift;
keep f f_std p arl_f;
set Turblim;
df = _limitn_ - 1;
do f = 1 to 1.5 by 0.05;
f_std = f * _stddev_;
low = df * ( _lcls_ / f_std )**2;
upp = df * ( _ucls_ / f_std )**2;
p = probchi( low, df ) + 1 - probchi( upp, df );
arl_f = 1 / p;
output;
end;
run;
The data set ARLshift is listed in Output 13.30.2. For example, on average, 53 samples are required to detect a ten percent increase in  (a shifted standard deviation of approximately 219). The computations use the fact that
(a shifted standard deviation of approximately 219). The computations use the fact that 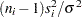 has a
has a 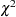 distribution with
distribution with 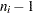 degrees of freedom, assuming that the measurements are normally distributed.
degrees of freedom, assuming that the measurements are normally distributed.
| Average Run Length Analysis |
| f | f_std | p | arl_f |
|---|---|---|---|
| 1.00 | 198.996 | 0.00279 | 358.073 |
| 1.05 | 208.945 | 0.00758 | 131.922 |
| 1.10 | 218.895 | 0.01875 | 53.322 |
| 1.15 | 228.845 | 0.03984 | 25.102 |
| 1.20 | 238.795 | 0.07388 | 13.535 |
| 1.25 | 248.745 | 0.12239 | 8.171 |
| 1.30 | 258.694 | 0.18475 | 5.413 |
| 1.35 | 268.644 | 0.25834 | 3.871 |
| 1.40 | 278.594 | 0.33923 | 2.948 |
| 1.45 | 288.544 | 0.42298 | 2.364 |
| 1.50 | 298.494 | 0.50546 | 1.978 |
Copyright © SAS Institute, Inc. All Rights Reserved.