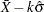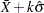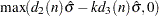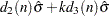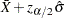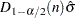| The SHEWHART Procedure |
Constructing Charts for Individual Measurements and Moving Ranges
The following notation is used in this section:
|
process mean (expected value of the population of measurements) |
||||
|
process standard deviation (standard deviation of the population of measurements) |
||||
|
the |
||||
|
mean of the individual measurements, computed as |
||||
|
number of consecutive measurements used to calculate the moving ranges (by default, |
||||
|
moving range computed for the
This formula assumes that |
||||
|
average of the nonmissing moving ranges, computed as
|
||||
|
expected value of the range of |
||||
|
standard error of the range of |
||||
|
100 |
||||
|
100 |
Plotted Points
Each point on an individual measurements chart, indicates the value of a measurement (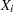 ).
).
Each point on a moving range chart indicates the value of a moving range (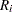 ). With
). With 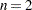 , for example, if the first three measurements are 3.4, 3.7, and 3.6, the first moving range is missing, the second moving range is
, for example, if the first three measurements are 3.4, 3.7, and 3.6, the first moving range is missing, the second moving range is  , and the third moving range is
, and the third moving range is 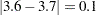 .
.
Central Lines
By default, the central line on an individual measurements chart indicates an estimate for 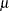 , which is computed as
, which is computed as 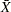 . If you specify a known value (
. If you specify a known value (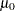 ) for
) for 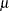 , the central line indicates the value of
, the central line indicates the value of 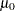 .
.
The central line on a moving range chart indicates an estimate for the expected moving range, computed as 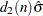 where
where 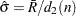 . If you specify a known value (
. If you specify a known value (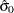 ) for
) for  , the central line indicates the value of
, the central line indicates the value of  .
.
Control Limits
You can compute the limits
as a specified multiple (
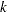 ) of the standard errors of
) of the standard errors of 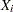 and
and 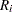 above and below the central line. The default limits are computed with
above and below the central line. The default limits are computed with 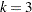 (these are referred to as
(these are referred to as 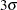 limits).
limits). as probability limits defined in terms of
 , a specified probability that
, a specified probability that 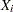 or
or 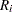 exceeds the limits
exceeds the limits
The following table provides the formulas for the limits:
Control Limits |
|
|---|---|
Individual Measurements Chart |
LCL |
UCL |
|
Moving Range Chart |
LCL |
UCL |
|
Probability Limits |
|
|---|---|
Individual Measurements Chart |
LCL |
UCL |
|
Moving Range Chart |
LCL |
UCL |
|
The formulas assume that the measurements are normally distributed. Note that the probability limits for the moving range are asymmetric about the central line. If standard values 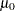 and
and 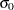 are available for
are available for 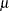 and
and  , replace
, replace 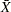 with
with 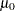 and
and 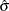 with
with 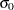 in Table 13.20.
in Table 13.20.
You can specify parameters for the limits as follows:
Specify
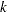 with the SIGMAS= option or with the variable _SIGMAS_ in a LIMITS= data set.
with the SIGMAS= option or with the variable _SIGMAS_ in a LIMITS= data set. Specify
 with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set.
with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set. Specify
 with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set.
with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set. Specify
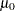 with the MU0= option or with the variable _MEAN_ in the LIMITS= data set.
with the MU0= option or with the variable _MEAN_ in the LIMITS= data set. Specify
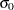 with the SIGMA0= option or with the variable _STDDEV_ in the LIMITS= data set.
with the SIGMA0= option or with the variable _STDDEV_ in the LIMITS= data set.
Copyright © SAS Institute, Inc. All Rights Reserved.
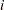 th individual measurement
th individual measurement  , where
, where 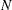 is the number of individual measurements
is the number of individual measurements 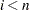 , then
, then 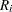 is assigned a missing value. Otherwise,
is assigned a missing value. Otherwise, 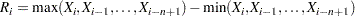
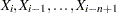 are nonmissing.
are nonmissing. 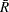

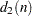
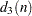
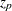
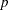 th percentile
th percentile 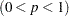 of the standard normal distribution
of the standard normal distribution 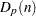
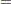 lower control limit =
lower control limit =