| The RELIABILITY Procedure |
| Regression Model with Two Independent Variables |
Meeker and Escobar (1998, p. 447) analyzed data from an accelerated test on the lifetimes of glass capacitors as a function of operating voltage and temperature. The following SAS statements create a SAS data set containing the data. There are four lifetimes for each of eight combinations and four censored observations after the fourth failure for each combination:
data glass;
input Temp Voltage @;
do i = 1 to 4;
cen = 0;
input Hours @; output;
end;
do i = 1 to 4;
cen = 1;
output;
end;
datalines;
170 200 439 904 1092 1105
170 250 572 690 904 1090
170 300 315 315 439 628
170 350 258 258 347 588
180 200 959 1065 1065 1087
180 250 216 315 455 473
180 300 241 315 332 380
180 350 241 241 435 455
;
run;
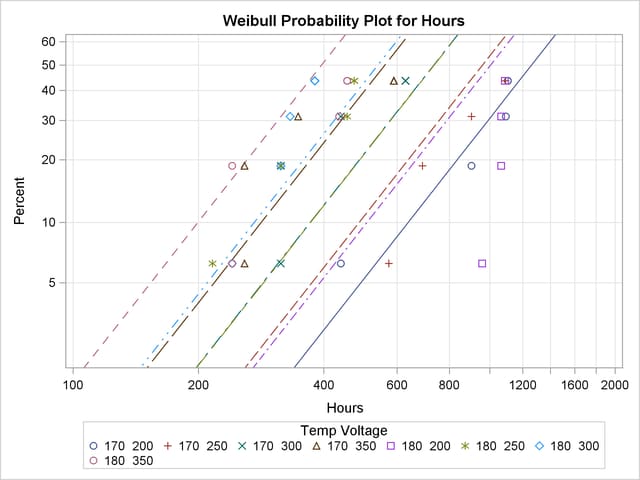
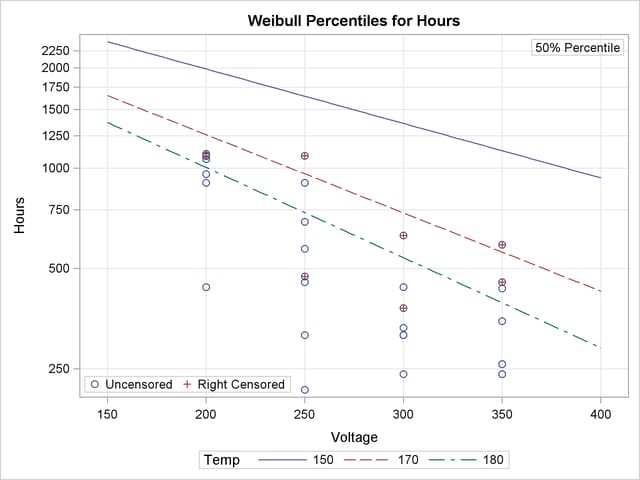
The following statements analyze the capacitor data. The MODEL statement fits a regression model with Temp and Voltage as independent variables. Parameter estimates from the fitted regression model are shown in Figure 12.24. An interaction term between Temp and Voltage is included. The PPLOT statement creates a Weibull probability plot shown in Figure 12.25 with all temperature-voltage combinations overlaid on the same plot. The regression model fit is also plotted. The RPLOT statement creates the plot shown in Figure 12.26 of the data and Weibull distribution percentiles from the regression model as a function of voltage for values of temperature of 150, 170, and 180:
proc reliability data = glass;
distribution Weibull;
model Hours*cen(1) = temp voltage temp * voltage;
pplot Hours*cen(1) = ( temp voltage ) / fit = model
overlay
noconf
lupper = 2000;
run;
proc reliability data = glass;
distribution Weibull;
model Hours*cen(1) = temp voltage temp * voltage;
rplot Hours*cen(1) = voltage / fit = regression(temp = 150, 170, 180)
plotfit;
run;
| Weibull Parameter Estimates | ||||
|---|---|---|---|---|
| Parameter | Estimate | Standard Error | Asymptotic Normal | |
| 95% Confidence Limits | ||||
| Lower | Upper | |||
| Intercept | 9.4135 | 10.5402 | -11.2449 | 30.0719 |
| Temp | -0.0062 | 0.0598 | -0.1235 | 0.1110 |
| Voltage | 0.0086 | 0.0374 | -0.0648 | 0.0820 |
| Temp*Voltage | -0.0001 | 0.0002 | -0.0005 | 0.0003 |
| EV Scale | 0.3624 | 0.0553 | 0.2687 | 0.4887 |
| Weibull Shape | 2.7593 | 0.4210 | 2.0461 | 3.7209 |
Copyright © SAS Institute, Inc. All Rights Reserved.