PROC OPTEX: Optimal Design Using a Small Candidate Set

The OPTEX Procedure

Example 10.5 Optimal Design Using a Small Candidate Set

[See OPTEX4 in the SAS/QC Sample Library]This example is a continuation of Example 10.4.

A well-chosen initial design can speed up the search procedure, as illustrated in Example 10.2. Another way to speed up the search is to reduce the candidate set. The following statements generate the optimal design with a fast, sequential search and then use the FREQ procedure to examine the frequency of different factor levels in the final design:

proc optex data=a seed=33805 noprint;
   model AFR|EGR|SA@2 AFR*AFR EGR*EGR SA*SA;
   generate n=50 method=sequential;
   output out=b;
proc freq;
   table AFR EGR SA / nocum;
run;

Output 10.5.1 Factor-Level Frequencies for Sequential Design

The FREQ Procedure

AFR	Frequency	Percent
15	19	38.00
16	6	12.00
17	6	12.00
18	19	38.00

EGR	Frequency	Percent
0.02	20	40.00
0.566	9	18.00
1.117	21	42.00

SA	Frequency	Percent
10	19	38.00
28	6	12.00
34	5	10.00
52	20	40.00

From Output 10.5.1, it is evident that most of the factor values lie in the middle or at the extremes of their respective ranges. This suggests looking for an optimal design with a candidate set that includes only those points in which the factors have values in the middle or at the extremes of their respective ranges. The following statements illustrate this approach (see Output 10.5.2):

proc plan;
   factors AFR=4 ordered EGR=4 ordered SA=4 ordered
           / noprint;
   output out=a AFR nvals=(15, 16, 17, 18)
                EGR nvals=(0.020, 0.377, 0.566, 1.117)
                SA  nvals=(10, 28, 34, 52);
proc optex seed=61552;
   model AFR|EGR|SA@2 AFR*AFR EGR*EGR SA*SA;
   generate n=50 method=detmax;
run;

Output 10.5.2 Optimal Design Using a Smaller Candidate Set

The OPTEX Procedure

Design Number	D-Efficiency	A-Efficiency	G-Efficiency	Average Prediction Standard Error
1	46.5151	24.9003	96.7226	0.4442
2	46.4997	24.5549	96.1157	0.4478
3	46.4920	24.5530	95.9941	0.4480
4	46.4657	24.8653	95.5627	0.4446
5	46.4547	24.5071	96.0385	0.4481
6	46.4333	25.0321	95.1371	0.4448
7	46.4333	25.0321	95.1371	0.4448
8	46.4333	25.0321	95.1371	0.4448
9	46.3916	24.3617	95.0041	0.4489
10	46.3379	24.8695	94.3115	0.4458

The resulting design is about as good as the best one obtained from a complete candidate set (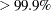 $\text{[math]}$ relative D-efficiency and marginally higher relative A-efficiency) and takes much less time to find.

See the section Handling Many Variables for another example of reducing the candidate set for the optimal design search.

Top of Page