| The OPTEX Procedure |
Example 10.1 Nonstandard Linear Model
[See OPTEX3 in the SAS/QC Sample Library]The following example is based on an example in Mitchell (1974a). An animal scientist wants to compare wildlife densities in four different habitats over a year. However, due to the cost of experimentation, only 12 observations can be made. The following model is postulated for the density 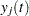 in habitat
in habitat 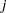 during month
during month  :
:
 |
 |
 |
This model includes the habitat as a classification variable, the effect of time with an overall linear drift term 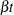 , and cyclic behavior in the form of a Fourier series. There is no intercept term in the model.
, and cyclic behavior in the form of a Fourier series. There is no intercept term in the model.
The OPTEX procedure is used since there are no standard designs that cover this situation. The candidate set is the full factorial arrangement of four habitats by 12 months, which can be generated with a DATA step, as follows:
data a;
drop theta pi;
array c{4} c1-c4;
array s{3} s1-s3;
pi = arcos(-1);
do Habitat=1 to 4;
do Month=1 to 12;
theta = pi * Month / 4;
do i=1 to 4; c{i} = cos(i*theta); end;
do i=1 to 3; s{i} = sin(i*theta); end;
output;
end;
end;
run;
Data set a contains the 48 candidate points and includes the four cosine variables (c1, c2, c3, and c4) and three sine variables (s1, s2, and s3). The following statements produce Output 10.1.1:
proc optex seed=193030034 data=a; class Habitat; model Habitat Month c1-c4 s1-s3 / noint; generate n=12; run;
| Design Number | D-Efficiency | A-Efficiency | G-Efficiency | Average Prediction Standard Error |
|---|---|---|---|---|
| 1 | 31.6103 | 19.7379 | 57.7350 | 1.3229 |
| 2 | 31.6103 | 19.7379 | 57.7350 | 1.3229 |
| 3 | 31.6103 | 19.7379 | 57.7350 | 1.3229 |
| 4 | 31.6103 | 19.3793 | 57.7350 | 1.3229 |
| 5 | 31.6103 | 19.2916 | 57.7350 | 1.3229 |
| 6 | 31.6103 | 19.0335 | 57.7350 | 1.3229 |
| 7 | 30.1304 | 14.8837 | 44.7214 | 1.4907 |
| 8 | 30.1304 | 14.2433 | 44.7214 | 1.5092 |
| 9 | 30.1304 | 13.1687 | 44.7214 | 1.5456 |
| 10 | 28.1616 | 9.8842 | 40.8248 | 1.7559 |
The best determinant (D-efficiency) was found in 6 out of the 10 tries. Thus, you can be confident that this is the best achievable determinant. Only the A-efficiency distinguishes among the designs listed in Output 10.1.1. The best design has an A-efficiency of 19.74%, whereas another design has the same D-efficiency but a slightly smaller A-efficiency of 19.03%, or about 96% relative A-efficiency. To explore the differences, you can save the designs in data sets and print them. Since the OPTEX procedure is interactive, you need to submit only the following statements (immediately after the preceding statements) to produce Output 10.1.2 and Output 10.1.3:
output out=d1 number=1; run; output out=d6 number=6; run; proc sort data=d1; by Month Habitat; proc print data=d1; var Month Habitat; run;
proc sort data=d6; by Month Habitat; proc print data=d6; var Month Habitat; run;
| Class Level Information | |||||
|---|---|---|---|---|---|
| Class | Levels | Values | |||
| Habitat | 4 | 1 | 2 | 3 | 4 |
| Factor Ranges | ||
|---|---|---|
| Factor | Low Value | High Value |
| Month | 1.000000 | 12.000000 |
| c1 | -1.000000 | 1.000000 |
| c2 | -1.000000 | 1.000000 |
| c3 | -1.000000 | 1.000000 |
| c4 | -1.000000 | 1.000000 |
| s1 | -1.000000 | 1.000000 |
| s2 | -1.000000 | 1.000000 |
| s3 | -1.000000 | 1.000000 |
| Design Number | D-Efficiency | A-Efficiency | G-Efficiency | Average Prediction Standard Error |
|---|---|---|---|---|
| 1 | 31.6103 | 19.7379 | 57.7350 | 1.3229 |
| 2 | 31.6103 | 19.7379 | 57.7350 | 1.3229 |
| 3 | 31.6103 | 19.7379 | 57.7350 | 1.3229 |
| 4 | 31.6103 | 19.3793 | 57.7350 | 1.3229 |
| 5 | 31.6103 | 19.2916 | 57.7350 | 1.3229 |
| 6 | 31.6103 | 19.0335 | 57.7350 | 1.3229 |
| 7 | 30.1304 | 14.8837 | 44.7214 | 1.4907 |
| 8 | 30.1304 | 14.2433 | 44.7214 | 1.5092 |
| 9 | 30.1304 | 13.1687 | 44.7214 | 1.5456 |
| 10 | 28.1616 | 9.8842 | 40.8248 | 1.7559 |
Note the structure of the best design in Output 10.1.2. One habitat is sampled in each month, each habitat is sampled three times, and the habitats are sampled in consecutive complete blocks. Even though the design in Output 10.1.3 is as D-efficient as the best, it has almost none of this structure; one habitat is sampled each month, but habitats are not sampled an equal number of times. This demonstrates the importance of choosing a final design on the basis of more than one criterion.
You can try searching for the A-optimal design directly. This takes more time but (with only 48 candidate points) is not too large a problem. The following statements produce Output 10.1.4:
proc optex seed=193030034 data=a; class Habitat; model Habitat Month c1-c4 s1-s3 / noint; generate n=12 criterion=A; run;
| Design Number | D-Efficiency | A-Efficiency | G-Efficiency | Average Prediction Standard Error |
|---|---|---|---|---|
| 1 | 31.6103 | 19.7379 | 57.7350 | 1.3229 |
| 2 | 30.1304 | 17.8273 | 52.2233 | 1.3894 |
| 3 | 30.1304 | 17.7943 | 52.2233 | 1.3944 |
| 4 | 30.1304 | 17.6471 | 52.2233 | 1.4093 |
| 5 | 28.1616 | 15.7055 | 44.7214 | 1.4860 |
| 6 | 28.1616 | 14.5289 | 44.7214 | 1.5343 |
| 7 | 28.1616 | 13.8603 | 39.2232 | 1.5811 |
| 8 | 25.0891 | 11.6152 | 37.7964 | 1.8143 |
| 9 | 25.0891 | 10.7563 | 37.7964 | 1.8143 |
| 10 | 25.0891 | 10.5437 | 33.3333 | 1.8930 |
The best design found is no more A-efficient than the one found previously.
Copyright © SAS Institute, Inc. All Rights Reserved.