| The GAGE Application |
| Average and Range Method |
The average and range method is widely used in industry because its calculations can be done by hand. It measures both repeatability and reproducibility for a measurement system.
All calculations described here are based upon a specified multiple of  , where the multiple
, where the multiple  can be 4, 5.15, or 6. Figure A.23 shows a sample gage report created with the GAGE application using the average and range method.
can be 4, 5.15, or 6. Figure A.23 shows a sample gage report created with the GAGE application using the average and range method.
The measure of repeatability (or equipment variation), denoted by  , is calculated as
, is calculated as
 |
where 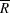 is the average range and
is the average range and 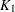 is the adjustment factor
is the adjustment factor
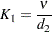 |
Average and Range Method
Test ID: Gasket Performed By:
Date: 04/17/02 John Smith
Part No. & Name: Gasket
Characteristics:
Specification: 0.6-1.0 mm
Gage Name: Thickness
Gage No.: X-2034
Gage Type: 0-10 mm
MEASUREMENT UNIT ANALYSIS % PROCESS VARIATION
Repeatability
EV = 0.1747 % EV = 18.70 %
Reproducibility
AV = 0.1570 % AV = 16.80 %
Gage R&R;
R&R; = 0.2349 % R&R; = 25.14 %
Part Variation
PV = 0.9042 % PV = 96.79 %
Total Variation
TV = 0.9342
Results are based upon predicting 5.15 sigma.
(99.0% of the area under the normal distribution curve)
The quantity 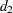 (Duncan 1974, Table M) depends on the number of trials used to calculate a single range. In the GAGE application, the number of trials can vary from 2 to 4. Use of
(Duncan 1974, Table M) depends on the number of trials used to calculate a single range. In the GAGE application, the number of trials can vary from 2 to 4. Use of 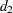 is valid when
is valid when 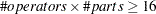 ; otherwise, the GAGE application uses
; otherwise, the GAGE application uses 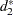 (Duncan 1974, Table D3), which is based on the number of ranges calculated from
(Duncan 1974, Table D3), which is based on the number of ranges calculated from 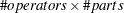 and on the number of trials.
and on the number of trials.
The measure of reproducibility (or appraiser variation), denoted by 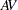 , is calculated as
, is calculated as
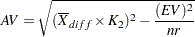 |
where 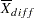 is the difference between the maximum operator average and the minimum operator average,
is the difference between the maximum operator average and the minimum operator average, 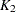 is the adjustment factor
is the adjustment factor
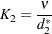 |
 is the number of parts, and
is the number of parts, and  is the number of trials. Reproducibility is contaminated by gage error and is adjusted by subtracting
is the number of trials. Reproducibility is contaminated by gage error and is adjusted by subtracting  . The quantity
. The quantity 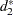 (Duncan 1974, Table D3) depends on the number of operators used to calculate a single range. In the GAGE application, the number of operators can vary from 1 to 4. When there is only one operator, reproducibility is set to zero.
(Duncan 1974, Table D3) depends on the number of operators used to calculate a single range. In the GAGE application, the number of operators can vary from 1 to 4. When there is only one operator, reproducibility is set to zero.
The measure of repeatability and reproducibility, denoted by 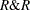 , is calculated as
, is calculated as
 |
Part-to-part variation, denoted by 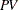 , is calculated as
, is calculated as
 |
where 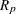 is the range of part averages and
is the range of part averages and 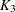 is the adjustment factor
is the adjustment factor
 |
Here the quantity 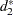 (Duncan 1974, Table D3) depends on the number of parts used to calculate a single range. In the GAGE application, the number of parts can vary from 2 to 15.
(Duncan 1974, Table D3) depends on the number of parts used to calculate a single range. In the GAGE application, the number of parts can vary from 2 to 15.
Total variation, denoted by  , is based on gage R&R and part-to-part variation.
, is based on gage R&R and part-to-part variation.
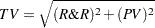 |
The measures of repeatability, reproducibility, gage R&R, part variation, and total variation are shown in Figure A.23 under the heading "MEASUREMENT UNIT ANALYSIS." The right-hand side of the report shows the "% PROCESS VARIATION" analysis, which compares the gage factors to total variation. The percent of total variation accounted for by each factor is calculated as follows:
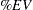 |
 |
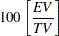 |
|||
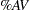 |
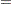 |
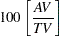 |
|||
 |
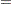 |
 |
|||
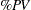 |
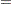 |
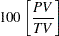 |
Note that the sum of these percentages does not equal 100%. You can use these percentages to determine whether the measurement system is acceptable for its intended application.
Instead of percent of process variation, your analysis may be based on percent of tolerance. For this you must specify a tolerance value. Then 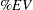 ,
,  ,
,  , and
, and 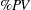 are calculated by substituting the tolerance value for
are calculated by substituting the tolerance value for  (the denominator) in the preceding formulas. A sample report with "% TOLERANCE ANALYSIS" is shown in Figure A.24.
(the denominator) in the preceding formulas. A sample report with "% TOLERANCE ANALYSIS" is shown in Figure A.24.
What is considered acceptable for  ? Barrentine (1991) gives the following guidelines:
? Barrentine (1991) gives the following guidelines:
10% or less |
excellent |
11% to 20% |
adequate |
21% to 30% |
marginally acceptable |
over 30% |
unacceptable |
In general, interpretation may be guided by local standards.
Average and Range Method
Test ID: Gasket Performed By:
Date: 04/17/02 John Smith
Part No. & Name: Gasket
Characteristics:
Specification: 0.6-1.0 mm
Gage Name: Thickness
Gage No.: X-2034
Gage Type: 0-10 mm Tolerance: 0.4
MEASUREMENT UNIT ANALYSIS % TOLERANCE ANALYSIS
Repeatability
EV = 0.1747 % EV = 43.68 %
Reproducibility
AV = 0.1570 % AV = 39.25 %
Gage R&R;
R&R; = 0.2349 % R&R; = 58.72 %
Part Variation
PV = 0.9042 % PV = 226.05 %
Total Variation
TV = 0.9342
Results are based upon predicting 5.15 sigma.
(99.0% of the area under the normal distribution curve)
Copyright © SAS Institute, Inc. All Rights Reserved.