The FREQ Procedure
Example 3.7 Cochran-Mantel-Haenszel Statistics
The data set Migraine contains hypothetical data for a clinical trial of migraine treatment. Subjects of both genders receive either a new drug
therapy or a placebo. Their response to treatment is coded as 'Better' or 'Same'. The data are recorded as cell counts, and
the number of subjects for each treatment and response combination is recorded in the variable Count.
data Migraine; input Gender $ Treatment $ Response $ Count @@; datalines; female Active Better 16 female Active Same 11 female Placebo Better 5 female Placebo Same 20 male Active Better 12 male Active Same 16 male Placebo Better 7 male Placebo Same 19 ;
The following PROC FREQ statements create a multiway table stratified by Gender, where Treatment forms the rows and Response forms the columns. The RELRISK option in the TABLES statement requests the odds ratio and relative risks for the two-way
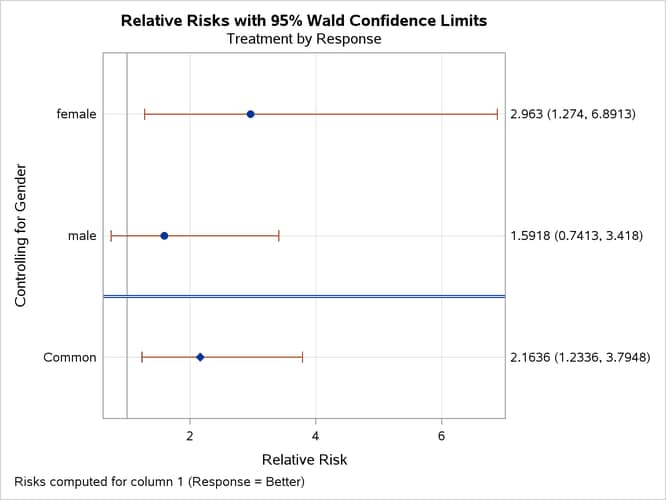
tables of Treatment by Response. The PLOTS= option requests a relative risk plot, which shows the relative risk and its confidence limits for each level
of Gender and overall. The CMH option requests Cochran-Mantel-Haenszel statistics for the multiway table. For this stratified table, the CMH option also produces estimates of the common relative risk and the Breslow-Day test for homogeneity of the
odds ratios. The NOPRINT option suppresses the display of the crosstabulation tables.
ods graphics on;
proc freq data=Migraine;
tables Gender*Treatment*Response /
relrisk plots(only)=relriskplot(stats) cmh noprint;
weight Count;
title 'Clinical Trial for Treatment of Migraine Headaches';
run;
ods graphics off;
Output 3.7.1 through Output 3.7.4 show the results of the analysis. The relative risk plot (Output 3.7.1) displays the relative risks and confidence limits for the two levels of Gender and for the overall (common) relative risk. Output 3.7.2 displays the CMH statistics. For a stratified table, the three CMH statistics test the same hypothesis. The significant p-value (0.004) indicates that the association between treatment and response remains strong after adjusting for gender.
The CMH option also produces a table of overall relative risks, as shown in Output 3.7.3. Because this is a prospective study, the relative risk estimate assesses the effectiveness of the new drug; the "Cohort (Col1 Risk)" values are the appropriate estimates for the first column (the risk of improvement). The probability of migraine improvement with the new drug is just over two times the probability of improvement with the placebo.
The large p-value for the Breslow-Day test (0.2218) in Output 3.7.4 indicates no significant gender difference in the odds ratios.
Output 3.7.1: Relative Risk Plot
Output 3.7.2: Cochran-Mantel-Haenszel Statistics
Output 3.7.3: CMH Option: Common Relative Risks
| Common Odds Ratio and Relative Risks | ||||
|---|---|---|---|---|
| Statistic | Method | Value | 95% Confidence Limits | |
| Odds Ratio | Mantel-Haenszel | 3.3132 | 1.4456 | 7.5934 |
| Logit | 3.2941 | 1.4182 | 7.6515 | |
| Relative Risk (Column 1) | Mantel-Haenszel | 2.1636 | 1.2336 | 3.7948 |
| Logit | 2.1059 | 1.1951 | 3.7108 | |
| Relative Risk (Column 2) | Mantel-Haenszel | 0.6420 | 0.4705 | 0.8761 |
| Logit | 0.6613 | 0.4852 | 0.9013 | |
Output 3.7.4: CMH Option: Breslow-Day Test
