The FREQ Procedure
Gail-Simon Test for Qualitative Interactions
The GAILSIMON option in the TABLES statement provides the Gail-Simon test for qualitative interaction for stratified 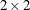 tables. For more information, see Gail and Simon (1985); Silvapulle (2001); Dmitrienko et al. (2005).
tables. For more information, see Gail and Simon (1985); Silvapulle (2001); Dmitrienko et al. (2005).
The Gail-Simon test is based on the risk differences in stratified 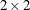 tables, where the risk difference is defined as the row 1 risk (proportion in column 1) minus the row 2 risk. For more information,
see the section Risks and Risk Differences. By default, PROC FREQ uses column 1 risks to compute the Gail-Simon test. If you specify the GAILSIMON(COLUMN=2) option,
PROC FREQ uses column 2 risks.
tables, where the risk difference is defined as the row 1 risk (proportion in column 1) minus the row 2 risk. For more information,
see the section Risks and Risk Differences. By default, PROC FREQ uses column 1 risks to compute the Gail-Simon test. If you specify the GAILSIMON(COLUMN=2) option,
PROC FREQ uses column 2 risks.
PROC FREQ computes the Gail-Simon test statistics as described in Gail and Simon (1985),
![\begin{eqnarray*} Q- & =& \sum _ h ~ (d_ h / s_ h)^2 ~ I(d_ h > 0 ) \\[0.10in] Q+ & =& \sum _ h ~ (d_ h / s_ h)^2 ~ I( d_ h < 0 ) \\[0.10in] Q & =& \min ~ (Q-, ~ Q+) \end{eqnarray*}](images/procstat_freq0659.png)
where 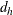 is the risk difference in table h,
is the risk difference in table h, 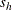 is the standard error of the risk difference, and
is the standard error of the risk difference, and 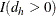 equals 1 if
equals 1 if 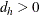 and 0 otherwise. Similarly,
and 0 otherwise. Similarly, 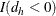 equals 1 if
equals 1 if 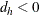 and 0 otherwise. The q
and 0 otherwise. The q 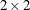 tables (strata) are indexed by
tables (strata) are indexed by 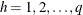 .
.
The p-values for the Gail-Simon statistics are computed as
![\begin{eqnarray*} p(Q-) & =& \sum _ h ~ (1 - F_ h(Q-)) ~ B(h; n=q, p=0.5) \\[0.10in] p(Q+) & =& \sum _ h ~ (1 - F_ h(Q+)) ~ B(h; n=q, p=0.5) \\[0.10in] p(Q) & =& \sum _{h=1}^{q-1} ~ (1-F_ h(Q)) ~ B(h; n=(q-1), p=0.5) \end{eqnarray*}](images/procstat_freq0666.png)
where 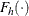 is the cumulative chi-square distribution function with h degrees of freedom and
is the cumulative chi-square distribution function with h degrees of freedom and 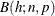 is the binomial probability function with parameters n and p. The statistic Q tests the null hypothesis of no qualitative interaction. The statistic
is the binomial probability function with parameters n and p. The statistic Q tests the null hypothesis of no qualitative interaction. The statistic 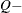 tests the null hypothesis of positive risk differences. A small p-value for
tests the null hypothesis of positive risk differences. A small p-value for 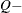 indicates negative differences; similarly, a small p-value for
indicates negative differences; similarly, a small p-value for 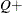 indicates positive risk differences.
indicates positive risk differences.
