The FREQ Procedure
Common Risk Difference
PROC FREQ provides Mantel-Haenszel and summary score estimates for the common risk (proportion) difference for multiway 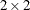 tables. PROC FREQ also provides stratified Newcombe confidence limits for the common risk difference.
tables. PROC FREQ also provides stratified Newcombe confidence limits for the common risk difference.
Mantel-Haenszel Estimate
PROC FREQ computes the Mantel-Haenszel (Mantel and Haenszel 1959) estimate of the common risk difference as
![\[ \hat{d}_{\mi{MH}} = \left( \sum _ h \hat{d}_ h w_ h \right) ~ / ~ \left( \sum _ h w_ h \right) \]](images/procstat_freq0374.png)
where  is the risk difference in stratum h and
is the risk difference in stratum h and
![\[ w_ h = n_{h1\cdot } n_{h2\cdot } / n_ h \]](images/procstat_freq0376.png)
The column 1 risk difference in stratum h is computed as
![\[ \hat{d}_ h = \hat{p}_{h1} - \hat{p}_{h2} = (n_{h11} / n_{h1 \cdot }) - (n_{h21} / n_{h2 \cdot }) \]](images/procstat_freq0377.png)
where  is the proportion of row 1 observations that are classified in column 1 and
is the proportion of row 1 observations that are classified in column 1 and  is the proportion or row 2 observations that are classified in column 1. The column 2 risk is computed in the same way. For
more information, see Agresti (2013, p. 231).
is the proportion or row 2 observations that are classified in column 1. The column 2 risk is computed in the same way. For
more information, see Agresti (2013, p. 231).
PROC FREQ computes the variance of  (Sato 1989) as
(Sato 1989) as
![\[ \hat{\sigma }^2(\hat{d}_{\mi{MH}}) = \left( \hat{d}_{\mi{MH}} \sum _ h P_ h + \sum _ h Q_ h \right) / \left( \sum _ h w_ h \right)^2 \]](images/procstat_freq0381.png)
where
![\[ P_ h = \left( n_{h1\cdot }^2 n_{h21} - n_{h2\cdot }^2 n_{h11} + n_{h1\cdot } n_{h2\cdot } (n_{h2\cdot }-n_{h1\cdot })/2 \right) / n_ h^2 \]](images/procstat_freq0382.png)
![\[ Q_ h = \left( n_{h11} ( n_{h2\cdot } - n_{h21} ) + n_{h21} (n_{h1\cdot } - n_{h11} ) \right) / 2 n_ h \]](images/procstat_freq0383.png)
The 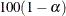 % confidence limits for the common risk difference are
% confidence limits for the common risk difference are
![\[ \hat{d}_{\mi{MH}} ~ \pm ~ \left( z_{\alpha /2} \times \hat{\sigma }(\hat{d}_{\mi{MH}}) \right) \]](images/procstat_freq0384.png)
Summary Score Estimate
PROC FREQ computes the summary score estimate of the common risk difference as described in Agresti (2013, p. 231). This estimate is computed from Miettinen-Nurminen (score) confidence limits for the stratum risk differences. For
more information, see the section "Miettinen-Nurminen (Score) Confidence Limits."
The score confidence interval for the risk difference in stratum h can be expressed as  , where
, where  is the midpoint of the score confidence interval and
is the midpoint of the score confidence interval and  is the width of the confidence interval divided by
is the width of the confidence interval divided by  . The summary score estimate of the common risk difference is computed as
. The summary score estimate of the common risk difference is computed as
![\[ \hat{d}_{\mi{S}} = \sum _ h \hat{d}_ h^\prime w_ h^\prime \]](images/procstat_freq0389.png)
where
![\[ w_ h^\prime = ( 1 / {s_ h^\prime }^2 ) / \sum _ i (1/{s_ i^\prime }^2) \]](images/procstat_freq0390.png)
The variance of  is computed as
is computed as
![\[ \hat{\sigma }^2(\hat{d}_{\mi{S}}) = 1 / \sum _ h ( 1 / {s_ h^\prime }^2 ) \]](images/procstat_freq0392.png)
The 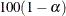 % summary score confidence limits for the common risk difference are
% summary score confidence limits for the common risk difference are
![\[ \hat{d}_{\mi{S}} ~ \pm ~ \left( z_{\alpha /2} \times \hat{\sigma }(\hat{d}_{\mi{S}}) \right) \]](images/procstat_freq0393.png)
Stratified Newcombe Confidence Limits
PROC FREQ computes stratified Newcombe confidence limits for the common risk (proportion) difference by using the method of Yan and Su (2010). The stratified Newcombe confidence limits are constructed from stratified Wilson confidence limits for the common (overall) row proportions.
PROC FREQ first computes individual Wilson confidence limits for the row proportions in each 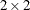 table (stratum), as described in the section Wilson (Score) Confidence Limits. These stratum Wilson confidence limits are then combined to form stratified Wilson confidence limits for the overall row
proportions by using Mantel-Haenszel weights, where the Mantel-Haenszel weight for stratum h is
table (stratum), as described in the section Wilson (Score) Confidence Limits. These stratum Wilson confidence limits are then combined to form stratified Wilson confidence limits for the overall row
proportions by using Mantel-Haenszel weights, where the Mantel-Haenszel weight for stratum h is
![\[ w_ h = n_{h1\cdot } n_{h2\cdot } / n_ h \]](images/procstat_freq0376.png)
The confidence levels of the stratum Wilson confidence limits are chosen so that the overall confidence coefficient (for
the stratified Wilson confidence limits) is 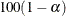 % (Yan and Su 2010).
% (Yan and Su 2010).
Denote the lower and upper stratified Wilson score confidence limits for the common row 1 proportion as 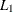 and
and 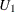 , respectively, and denote the lower and upper stratified Wilson confidence limits for the common row 2 proportion as
, respectively, and denote the lower and upper stratified Wilson confidence limits for the common row 2 proportion as 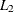 and
and 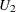 , respectively. The
, respectively. The 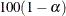 % stratified Newcombe confidence limits for the common risk (proportion) difference are
% stratified Newcombe confidence limits for the common risk (proportion) difference are
![\begin{eqnarray*} L & = & \hat{d}_{\mi{MH}} ~ - ~ z_{\alpha /2} \sqrt { \lambda _1 L_1 (1-L_1) + \lambda _2 U_2 (1-U_2) } \\[0.10in] U & = & \hat{d}_{\mi{MH}} ~ + ~ z_{\alpha /2} \sqrt { \lambda _2 L_2 (1-L_2) + \lambda _1 U_1 (1-U_1) } \end{eqnarray*}](images/procstat_freq0395.png)
where  is the Mantel-Haenszel estimate of the common risk difference and
is the Mantel-Haenszel estimate of the common risk difference and
![\begin{eqnarray*} \lambda _1 & = & \sum _ h w_ h^2 / n_{h1\cdot } \\[0.05in] \lambda _2 & = & \sum _ h w_ h^2 / n_{h2\cdot } \end{eqnarray*}](images/procstat_freq0396.png)
When there is a single stratum, the stratified Newcombe confidence interval is equivalent to the (unstratified) Newcombe confidence interval. For more information, see the subsection "Newcombe Confidence Limits" in the section Confidence Limits for the Risk Difference. See also Kim and Won (2013).
