The UNIVARIATE Procedure
- Overview
-
Getting Started
-
Syntax
-
DetailsMissing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources
-
ExamplesComputing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Plots for Line Printer OutputAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot
- References
In addition to summarizing a data distribution as in the preceding example, you can use PROC UNIVARIATE to statistically model
a distribution based on a random sample of data. The following statements create a data set named Aircraft that contains the measurements of a position deviation for a sample of 30 aircraft components.
data Aircraft; input Deviation @@; label Deviation = 'Position Deviation'; datalines; -.00653 0.00141 -.00702 -.00734 -.00649 -.00601 -.00631 -.00148 -.00731 -.00764 -.00275 -.00497 -.00741 -.00673 -.00573 -.00629 -.00671 -.00246 -.00222 -.00807 -.00621 -.00785 -.00544 -.00511 -.00138 -.00609 0.00038 -.00758 -.00731 -.00455 ;
An initial question in the analysis is whether the measurement distribution is normal. The following statements request a table of moments, the tests for normality, and a normal probability plot, which are shown in Figure 4.5 and Figure 4.6:
title 'Position Deviation Analysis';
ods graphics on;
ods select Moments TestsForNormality ProbPlot;
proc univariate data=Aircraft normaltest;
var Deviation;
probplot Deviation / normal (mu=est sigma=est)
square;
label Deviation = 'Position Deviation';
inset mean std / format=6.4;
run;
When ODS Graphics is enabled, the procedure produces ODS Graphics output rather than traditional graphics. (See the section Alternatives for Producing Graphics for information about traditional graphics and ODS Graphics.) The INSET statement displays the sample mean and standard deviation on the probability plot.
Figure 4.5: Moments and Tests for Normality
| Position Deviation Analysis |
| Moments | |||
|---|---|---|---|
| N | 30 | Sum Weights | 30 |
| Mean | -0.0053067 | Sum Observations | -0.1592 |
| Std Deviation | 0.00254362 | Variance | 6.47002E-6 |
| Skewness | 1.2562507 | Kurtosis | 0.69790426 |
| Uncorrected SS | 0.00103245 | Corrected SS | 0.00018763 |
| Coeff Variation | -47.932613 | Std Error Mean | 0.0004644 |
| Tests for Normality | ||||
|---|---|---|---|---|
| Test | Statistic | p Value | ||
| Shapiro-Wilk | W | 0.845364 | Pr < W | 0.0005 |
| Kolmogorov-Smirnov | D | 0.208921 | Pr > D | <0.0100 |
| Cramer-von Mises | W-Sq | 0.329274 | Pr > W-Sq | <0.0050 |
| Anderson-Darling | A-Sq | 1.784881 | Pr > A-Sq | <0.0050 |
All four goodness-of-fit tests in Figure 4.5 reject the hypothesis that the measurements are normally distributed.
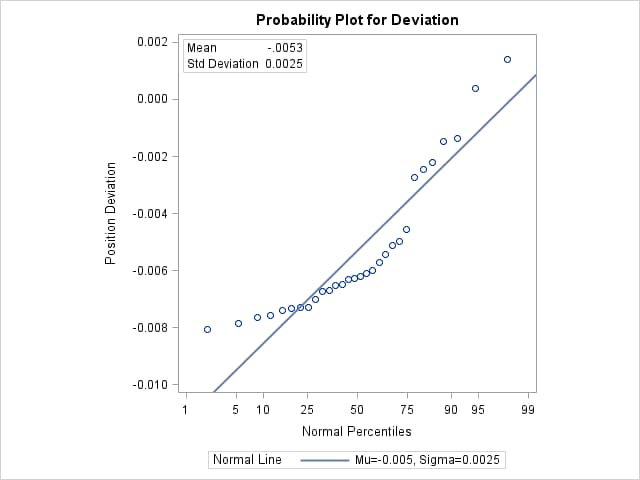
Figure 4.6 shows a normal probability plot for the measurements. A linear pattern of points following the diagonal reference line would indicate that the measurements are normally distributed. Instead, the curved point pattern suggests that a skewed distribution, such as the lognormal, is more appropriate than the normal distribution.
A lognormal distribution for Deviation is fitted in Example 4.26.
A sample program for this example, univar2.sas, is available in the SAS Sample Library for Base SAS software.
