The CORR Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Pearson Product-Moment Correlation Spearman Rank-Order Correlation Kendall’s Tau-b Correlation Coefficient Hoeffding Dependence Coefficient Partial Correlation Fisher’s z Transformation Polyserial Correlation Cronbach’s Coefficient Alpha Confidence and Prediction Ellipses Missing Values In-Database Computation Output Tables Output Data Sets ODS Table Names ODS Graphics
Pearson Product-Moment Correlation Spearman Rank-Order Correlation Kendall’s Tau-b Correlation Coefficient Hoeffding Dependence Coefficient Partial Correlation Fisher’s z Transformation Polyserial Correlation Cronbach’s Coefficient Alpha Confidence and Prediction Ellipses Missing Values In-Database Computation Output Tables Output Data Sets ODS Table Names ODS Graphics -
Examples
 Computing Four Measures of Association Computing Correlations between Two Sets of Variables Analysis Using Fisher’s z Transformation Applications of Fisher’s z Transformation Computing Polyserial Correlations Computing Cronbach’s Coefficient Alpha Saving Correlations in an Output Data Set Creating Scatter Plots Computing Partial Correlations
Computing Four Measures of Association Computing Correlations between Two Sets of Variables Analysis Using Fisher’s z Transformation Applications of Fisher’s z Transformation Computing Polyserial Correlations Computing Cronbach’s Coefficient Alpha Saving Correlations in an Output Data Set Creating Scatter Plots Computing Partial Correlations - References
| Fisher’s z Transformation |
For a sample correlation  that uses a sample from a bivariate normal distribution with correlation
that uses a sample from a bivariate normal distribution with correlation  , the statistic
, the statistic
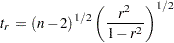 |
has a Student’s  distribution with (
distribution with (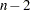 ) degrees of freedom.
) degrees of freedom.
With the monotone transformation of the correlation  (Fisher 1921)
(Fisher 1921)
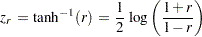 |
the statistic  has an approximate normal distribution with mean and variance
has an approximate normal distribution with mean and variance
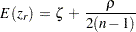 |
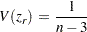 |
where 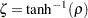 .
.
For the transformed 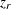 , the approximate variance
, the approximate variance 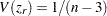 is independent of the correlation
is independent of the correlation  . Furthermore, even the distribution of
. Furthermore, even the distribution of 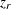 is not strictly normal, it tends to normality rapidly as the sample size increases for any values of
is not strictly normal, it tends to normality rapidly as the sample size increases for any values of  (Fisher 1970, pp. 200–201).
(Fisher 1970, pp. 200–201).
For the null hypothesis 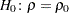 , the
, the 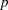 -values are computed by treating
-values are computed by treating
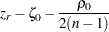 |
as a normal random variable with mean zero and variance 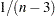 , where
, where 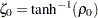 (Fisher 1970, p. 207; Anderson 1984, p. 123).
(Fisher 1970, p. 207; Anderson 1984, p. 123).
Note that the bias adjustment, 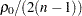 , is always used when computing
, is always used when computing 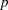 -values under the null hypothesis
-values under the null hypothesis 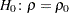 in the CORR procedure.
in the CORR procedure.
The ALPHA= option in the FISHER option specifies the value  for the confidence level
for the confidence level  , the RHO0= option specifies the value
, the RHO0= option specifies the value 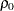 in the hypothesis
in the hypothesis 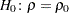 , and the BIASADJ= option specifies whether the bias adjustment is to be used for the confidence limits.
, and the BIASADJ= option specifies whether the bias adjustment is to be used for the confidence limits.
The TYPE= option specifies the type of confidence limits. The TYPE=TWOSIDED option requests two-sided confidence limits and a 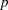 -value under the hypothesis
-value under the hypothesis 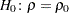 . For a one-sided confidence limit, the TYPE=LOWER option requests a lower confidence limit and a
. For a one-sided confidence limit, the TYPE=LOWER option requests a lower confidence limit and a 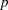 -value under the hypothesis
-value under the hypothesis 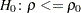 , and the TYPE=UPPER option requests an upper confidence limit and a
, and the TYPE=UPPER option requests an upper confidence limit and a 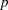 -value under the hypothesis
-value under the hypothesis  .
.
Confidence Limits for the Correlation
The confidence limits for the correlation  are derived through the confidence limits for the parameter
are derived through the confidence limits for the parameter 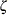 , with or without the bias adjustment.
, with or without the bias adjustment.
Without a bias adjustment, confidence limits for 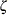 are computed by treating
are computed by treating
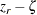 |
as having a normal distribution with mean zero and variance 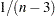 .
.
That is, the two-sided confidence limits for 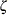 are computed as
are computed as
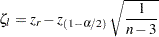 |
 |
where  is the
is the 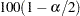 percentage point of the standard normal distribution.
percentage point of the standard normal distribution.
With a bias adjustment, confidence limits for 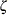 are computed by treating
are computed by treating
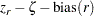 |
as having a normal distribution with mean zero and variance 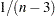 , where the bias adjustment function (Keeping 1962, p. 308) is
, where the bias adjustment function (Keeping 1962, p. 308) is
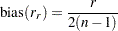 |
That is, the two-sided confidence limits for 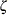 are computed as
are computed as
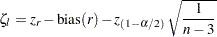 |
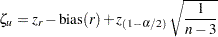 |
These computed confidence limits of  and
and  are then transformed back to derive the confidence limits for the correlation
are then transformed back to derive the confidence limits for the correlation  :
:
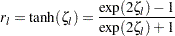 |
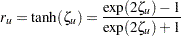 |
Note that with a bias adjustment, the CORR procedure also displays the following correlation estimate:
 |
Applications of Fisher’s z Transformation
Fisher (1970, p. 199) describes the following practical applications of the  transformation:
transformation:
testing whether a population correlation is equal to a given value
testing for equality of two population correlations
combining correlation estimates from different samples
To test if a population correlation  from a sample of
from a sample of 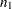 observations with sample correlation
observations with sample correlation 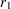 is equal to a given
is equal to a given 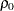 , first apply the
, first apply the  transformation to
transformation to 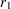 and
and 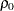 :
:  and
and 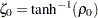 .
.
The 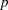 -value is then computed by treating
-value is then computed by treating
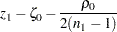 |
as a normal random variable with mean zero and variance 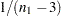 .
.
Assume that sample correlations 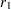 and
and 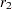 are computed from two independent samples of
are computed from two independent samples of 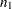 and
and 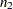 observations, respectively. To test whether the two corresponding population correlations,
observations, respectively. To test whether the two corresponding population correlations,  and
and 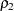 , are equal, first apply the
, are equal, first apply the  transformation to the two sample correlations:
transformation to the two sample correlations:  and
and 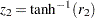 .
.
The 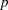 -value is derived under the null hypothesis of equal correlation. That is, the difference
-value is derived under the null hypothesis of equal correlation. That is, the difference 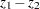 is distributed as a normal random variable with mean zero and variance
is distributed as a normal random variable with mean zero and variance  .
.
Assuming further that the two samples are from populations with identical correlation, a combined correlation estimate can be computed. The weighted average of the corresponding  values is
values is
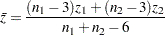 |
where the weights are inversely proportional to their variances.
Thus, a combined correlation estimate is 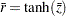 and
and 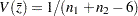 . See Example 2.4 for further illustrations of these applications.
. See Example 2.4 for further illustrations of these applications.
Note that this approach can be extended to include more than two samples.