| The UNIVARIATE Procedure |
Example 4.11 Computing Robust Estimates
This example illustrates how you can use the UNIVARIATE procedure to compute robust estimates of location and scale. The following statements compute these estimates for the variable Systolic in the data set BPressure, which was introduced in Example 4.1:
title 'Robust Estimates for Blood Pressure Data';
ods select TrimmedMeans WinsorizedMeans RobustScale;
proc univariate data=BPressure trimmed=1 .1
winsorized=.1 robustscale;
var Systolic;
run;
The ODS SELECT statement restricts the output to the "TrimmedMeans," "WinsorizedMeans," and "RobustScale" tables; see the section ODS Table Names. The TRIMMED= option computes two trimmed means, the first after removing one observation and the second after removing 10% of the observations. If the value of TRIMMED= is greater than or equal to one, it is interpreted as the number of observations to be trimmed. The WINSORIZED= option computes a Winsorized mean that replaces three observations from the tails with the next closest observations. (Three observations are replaced because 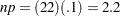 , and three is the smallest integer greater than 2.2.) The trimmed and Winsorized means for Systolic are displayed in Output 4.11.1.
, and three is the smallest integer greater than 2.2.) The trimmed and Winsorized means for Systolic are displayed in Output 4.11.1.
| Trimmed Means | ||||||||
|---|---|---|---|---|---|---|---|---|
| Percent Trimmed in Tail |
Number Trimmed in Tail |
Trimmed Mean |
Std Error Trimmed Mean |
95% Confidence Limits | DF | t for H0: Mu0=0.00 |
Pr > |t| | |
| 4.55 | 1 | 120.3500 | 2.573536 | 114.9635 | 125.7365 | 19 | 46.76446 | <.0001 |
| 13.64 | 3 | 120.3125 | 2.395387 | 115.2069 | 125.4181 | 15 | 50.22675 | <.0001 |
Output 4.11.1 shows the trimmed mean for Systolic is 120.35 after one observation has been trimmed, and 120.31 after 3 observations are trimmed. The Winsorized mean for Systolic is 120.64. For details on trimmed and Winsorized means, see the section Robust Estimators. The trimmed means can be compared with the means shown in Output 4.1.1 (from Example 4.1), which displays the mean for Systolic as 121.273.
The ROBUSTSCALE option requests a table, displayed in Output 4.11.2, which includes the interquartile range, Gini’s mean difference, the median absolute deviation about the median, 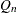 , and
, and 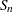 .
.
Output 4.11.2 shows the robust estimates of scale for Systolic. For instance, the interquartile range is 13. The estimates of  range from 9.54 to 13.32. See the section Robust Estimators.
range from 9.54 to 13.32. See the section Robust Estimators.
A sample program for this example, uniex01.sas, is available in the SAS Sample Library for Base SAS software.
Copyright © SAS Institute, Inc. All Rights Reserved.