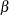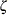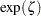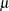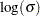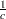| The UNIVARIATE Procedure |
| Estimating Location and Scale Parameters Using Q-Q Plots |
If you specify location and scale parameters for a distribution in a PROBPLOT or QQPLOT statement (or if you request estimates for these parameters), a diagonal distribution reference line is displayed on the plot. (An exception is the two-parameter Weibull distribution, for which a line is displayed when you specify or estimate the scale and shape parameters.) Agreement between this line and the point pattern indicates that the distribution with these parameters is a good fit.
When the point pattern on a Q-Q plot is linear, its intercept and slope provide estimates of the location and scale parameters. (An exception to this rule is the two-parameter Weibull distribution, for which the intercept and slope are related to the scale and shape parameters.)
Table 4.88 shows how the specified parameters determine the intercept and slope of the line. The intercept and slope are based on the quantile scale for the horizontal axis, which is used in Q-Q plots.
Parameters |
Linear Pattern |
||||
|---|---|---|---|---|---|
Distribution |
Location |
Scale |
Shape |
Intercept |
Slope |
Beta |
|
|
|
|
|
Exponential |
|
|
|
|
|
Gamma |
|
|
|
|
|
Lognormal |
|
|
|
|
|
Normal |
|
|
|
|
|
Weibull (3-parameter) |
|
|
|
|
|
Weibull (2-parameter) |
|
|
|
|
|
For instance, specifying MU=3 and SIGMA=2 with the NORMAL option requests a line with intercept 3 and slope 2. Specifying SIGMA=1 and C=2 with the WEIBULL2 option requests a line with intercept 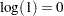 and slope
and slope  . On a probability plot with the LOGNORMAL and WEIBULL2 options, you can specify the slope directly with the SLOPE= option. That is, for the LOGNORMAL option, specifying THETA=
. On a probability plot with the LOGNORMAL and WEIBULL2 options, you can specify the slope directly with the SLOPE= option. That is, for the LOGNORMAL option, specifying THETA= 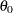 and SLOPE=
and SLOPE=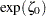 displays the same line as specifying THETA=
displays the same line as specifying THETA= 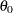 and ZETA=
and ZETA= 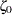 . For the WEIBULL2 option, specifying SIGMA=
. For the WEIBULL2 option, specifying SIGMA= 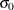 and SLOPE=
and SLOPE= 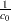 displays the same line as specifying SIGMA=
displays the same line as specifying SIGMA= 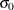 and C=
and C= 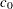 .
.
Copyright © SAS Institute, Inc. All Rights Reserved.
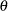

 ,
,