| The CORR Procedure |
Example 2.4 Applications of Fisher’s z Transformation
This example illustrates some applications of Fisher’s  transformation. For details, see the section Fisher’s z Transformation.
transformation. For details, see the section Fisher’s z Transformation.
The following statements simulate independent samples of variables X and Y from a bivariate normal distribution. The first batch of 150 observations is sampled using a known correlation of 0.3, the second batch of 150 observations is sampled using a known correlation of 0.25, and the third batch of 100 observations is sampled using a known correlation of 0.3.
data Sim (drop=i); do i=1 to 400; X = rannor(135791); Batch = 1 + (i>150) + (i>300); if Batch = 1 then Y = 0.3*X + 0.9*rannor(246791); if Batch = 2 then Y = 0.25*X + sqrt(.8375)*rannor(246791); if Batch = 3 then Y = 0.3*X + 0.9*rannor(246791); output; end; run;
This data set will be used to illustrate the following applications of Fisher’s  transformation:
transformation:
testing whether a population correlation is equal to a given value
testing for equality of two population correlations
combining correlation estimates from different samples
Testing Whether a Population Correlation Is Equal to a Given Value 
You can use the following statements to test the null hypothesis 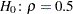 against a two-sided alternative
against a two-sided alternative 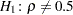 . The test is requested with the option FISHER(RHO0=0.5).
. The test is requested with the option FISHER(RHO0=0.5).
title 'Analysis for Batch 1'; proc corr data=Sim (where=(Batch=1)) fisher(rho0=.5); var X Y; run;
Output 2.4.1 displays the results based on Fisher’s transformation. The null hypothesis is rejected since the 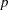 -value is less than
-value is less than 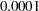 .
.
| Pearson Correlation Statistics (Fisher's z Transformation) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variable | With Variable | N | Sample Correlation | Fisher's z | Bias Adjustment | Correlation Estimate | H0:Rho=Rho0 | |||
| 95% Confidence Limits | Rho0 | p Value | ||||||||
| X | Y | 150 | 0.22081 | 0.22451 | 0.0007410 | 0.22011 | 0.062034 | 0.367409 | 0.50000 | <.0001 |
Testing for Equality of Two Population Correlations
You can use the following statements to test for equality of two population correlations, 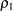 and
and 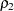 . Here, the null hypothesis
. Here, the null hypothesis 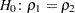 is tested against the alternative
is tested against the alternative 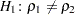 .
.
ods output FisherPearsonCorr=SimCorr; title 'Testing Equality of Population Correlations'; proc corr data=Sim (where=(Batch=1 or Batch=2)) fisher; var X Y; by Batch; run;
The ODS OUTPUT statement saves the "FisherPearsonCorr" table into an output data set in the CORR procedure. The output data set SimCorr contains Fisher’s  statistics for both batches.
statistics for both batches.
The following statements display (in Figure 2.4.2) the output data set SimCorr:
proc print data=SimCorr; run;
The 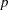 -value for testing
-value for testing 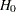 is derived by treating the difference
is derived by treating the difference 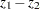 as a normal random variable with mean zero and variance
as a normal random variable with mean zero and variance 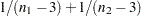 , where
, where  and
and 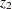 are Fisher’s
are Fisher’s  transformation of the sample correlations
transformation of the sample correlations 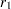 and
and 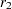 , respectively, and where
, respectively, and where 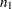 and
and 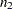 are the corresponding sample sizes.
are the corresponding sample sizes.
The following statements compute the 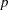 -value in Output 2.4.3:
-value in Output 2.4.3:
data SimTest (drop=Batch);
merge SimCorr (where=(Batch=1) keep=Nobs ZVal Batch
rename=(Nobs=n1 ZVal=z1))
SimCorr (where=(Batch=2) keep=Nobs ZVal Batch
rename=(Nobs=n2 ZVal=z2));
variance = 1/(n1-3) + 1/(n2-3);
z = (z1 - z2) / sqrt( variance );
pval = probnorm(z);
if (pval > 0.5) then pval = 1 - pval;
pval = 2*pval;
run;
proc print data=SimTest noobs;
run;
In Output 2.4.3, the 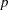 -value of 0.2795 does not provide evidence to reject the null hypothesis that
-value of 0.2795 does not provide evidence to reject the null hypothesis that 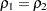 . The sample sizes
. The sample sizes 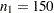 and
and 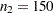 are not large enough to detect the difference
are not large enough to detect the difference 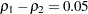 at a significance level of
at a significance level of  .
.
Combining Correlation Estimates from Different Samples
Assume that sample correlations 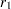 and
and 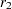 are computed from two independent samples of
are computed from two independent samples of 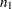 and
and 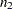 observations, respectively. A combined correlation estimate is given by
observations, respectively. A combined correlation estimate is given by 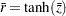 , where
, where 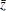 is the weighted average of the
is the weighted average of the  transformations of
transformations of 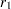 and
and 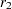 :
:
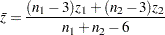 |
The following statements compute a combined estimate of 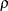 by using Batch 1 and Batch 3:
by using Batch 1 and Batch 3:
ods output FisherPearsonCorr=SimCorr2;
proc corr data=Sim (where=(Batch=1 or Batch=3)) fisher;
var X Y;
by Batch;
run;
data SimComb (drop=Batch);
merge SimCorr2 (where=(Batch=1) keep=Nobs ZVal Batch
rename=(Nobs=n1 ZVal=z1))
SimCorr2 (where=(Batch=3) keep=Nobs ZVal Batch
rename=(Nobs=n2 ZVal=z2));
z = ((n1-3)*z1 + (n2-3)*z2) / (n1+n2-6);
corr = tanh(z);
var = 1/(n1+n2-6);
zlcl = z - probit(0.975)*sqrt(var);
zucl = z + probit(0.975)*sqrt(var);
lcl= tanh(zlcl);
ucl= tanh(zucl);
pval= probnorm( z/sqrt(var));
if (pval > .5) then pval= 1 - pval;
pval= 2*pval;
run;
proc print data=SimComb noobs;
var n1 z1 n2 z2 corr lcl ucl pval;
run;
Output 2.4.4 displays the combined estimate of 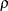 . The table shows that a correlation estimate from the combined samples is
. The table shows that a correlation estimate from the combined samples is 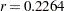 . The
. The 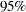 confidence interval is
confidence interval is  , using the variance of the combined estimate. Note that this interval contains the population correlation
, using the variance of the combined estimate. Note that this interval contains the population correlation 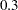 .
.
Copyright © SAS Institute, Inc. All Rights Reserved.
