Previous Page | Next Page

The CORR Procedure

Example 2.4 Applications of Fisher’s z Transformation

This example illustrates some applications of Fisher’s transformation. For details, see the section Fisher’s z Transformation.

The following statements simulate independent samples of variables X and Y from a bivariate normal distribution. The first batch of 150 observations is sampled using a known correlation of 0.3, the second batch of 150 observations is sampled using a known correlation of 0.25, and the third batch of 100 observations is sampled using a known correlation of 0.3. 

data Sim (drop=i);
do i=1 to 400;
  X = rannor(135791);
  Batch = 1 + (i>150) + (i>300);
  if Batch = 1 then Y = 0.3*X + 0.9*rannor(246791);
  if Batch = 2 then Y = 0.25*X + sqrt(.8375)*rannor(246791);
  if Batch = 3 then Y = 0.3*X + 0.9*rannor(246791);
  output;
end;
run;

This data set will be used to illustrate the following applications of Fisher’s transformation:

testing whether a population correlation is equal to a given value

testing for equality of two population correlations

combining correlation estimates from different samples

Testing Whether a Population Correlation Is Equal to a Given Value

You can use the following statements to test the null hypothesis against a two-sided alternative . The test is requested with the option FISHER(RHO0=0.5). 

title 'Analysis for Batch 1';
proc corr data=Sim (where=(Batch=1)) fisher(rho0=.5);
   var X Y;
run;

Output 2.4.1 displays the results based on Fisher’s transformation. The null hypothesis is rejected since the -value is less than .

Output 2.4.1 Fisher’s Test for
Analysis for Batch 1

The CORR Procedure

Pearson Correlation Statistics (Fisher's z Transformation)
Variable With Variable N Sample Correlation Fisher's z Bias Adjustment Correlation Estimate   H0:Rho=Rho0
95% Confidence Limits Rho0 p Value
X Y 150 0.22081 0.22451 0.0007410 0.22011 0.062034 0.367409 0.50000 <.0001

Testing for Equality of Two Population Correlations

You can use the following statements to test for equality of two population correlations, 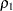and 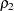. Here, the null hypothesis is tested against the alternative . 

ods output FisherPearsonCorr=SimCorr;
title 'Testing Equality of Population Correlations';
proc corr data=Sim (where=(Batch=1 or Batch=2)) fisher;
   var X Y;
   by Batch;
run;

The ODS OUTPUT statement saves the "FisherPearsonCorr" table into an output data set in the CORR procedure. The output data set SimCorr contains Fisher’s statistics for both batches.

The following statements display (in Figure 2.4.2) the output data set SimCorr: 

proc print data=SimCorr;   
run;

Output 2.4.2 Fisher’s Correlation Statistics
Obs Batch Var WithVar NObs Corr ZVal BiasAdj CorrEst Lcl Ucl pValue
1 1 X Y 150 0.22081 0.22451 0.0007410 0.22011 0.062034 0.367409 0.0065
2 2 X Y 150 0.33694 0.35064 0.00113 0.33594 0.185676 0.470853 <.0001

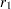The -value for testing is derived by treating the difference as a normal random variable with mean zero and variance , where and are Fisher’s transformation of the sample correlations and , respectively, and where and 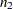are the corresponding sample sizes.

The following statements compute the -value in Output 2.4.3: 

data SimTest (drop=Batch);
   merge SimCorr (where=(Batch=1) keep=Nobs ZVal Batch 
                  rename=(Nobs=n1 ZVal=z1))
         SimCorr (where=(Batch=2) keep=Nobs ZVal Batch 
                  rename=(Nobs=n2 ZVal=z2));
   variance = 1/(n1-3) + 1/(n2-3);
   z = (z1 - z2) / sqrt( variance );
   pval = probnorm(z);
   if (pval > 0.5) then pval = 1 - pval;
   pval = 2*pval;
run;

proc print data=SimTest noobs;
run;

Output 2.4.3 Test of Equality of Observed Correlations
n1 z1 n2 z2 variance z pval
150 0.22451 150 0.35064 0.013605 -1.08135 0.27954

In Output 2.4.3, the -value of 0.2795 does not provide evidence to reject the null hypothesis that . The sample sizes and are not large enough to detect the difference at a significance level of .

Combining Correlation Estimates from Different Samples

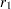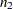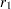Assume that sample correlations and are computed from two independent samples of and observations, respectively. A combined correlation estimate is given by , where is the weighted average of the transformations of and :

     

The following statements compute a combined estimate of 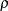by using Batch 1 and Batch 3: 

ods output FisherPearsonCorr=SimCorr2;
proc corr data=Sim (where=(Batch=1 or Batch=3)) fisher;
   var X Y;
   by Batch;
run;

data SimComb (drop=Batch);
   merge SimCorr2 (where=(Batch=1) keep=Nobs ZVal Batch 
                   rename=(Nobs=n1 ZVal=z1))
         SimCorr2 (where=(Batch=3) keep=Nobs ZVal Batch 
                   rename=(Nobs=n2 ZVal=z2));
   z = ((n1-3)*z1 + (n2-3)*z2) / (n1+n2-6);
   corr = tanh(z);
   var = 1/(n1+n2-6);
   zlcl = z - probit(0.975)*sqrt(var);
   zucl = z + probit(0.975)*sqrt(var);
   lcl= tanh(zlcl);
   ucl= tanh(zucl);
   pval= probnorm( z/sqrt(var));
   if (pval > .5)  then pval= 1 - pval;
   pval= 2*pval;
run;

proc print data=SimComb noobs;
   var n1 z1 n2 z2 corr lcl ucl pval;
run;

Output 2.4.4 displays the combined estimate of 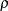. The table shows that a correlation estimate from the combined samples is . The confidence interval is , using the variance of the combined estimate. Note that this interval contains the population correlation .

Output 2.4.4 Combined Correlation Estimate
Obs n1 z1 n2 z2 z corr var zlcl zucl lcl ucl pval
1 150 0.22451 100 0.23929 0.23039 0.22640 .004098361 0.10491 0.35586 0.10453 0.34156 .000319748

Previous Page | Next Page | Top of Page

Copyright © SAS Institute, Inc. All Rights Reserved.