The HPBIN Procedure
For variable x, assume that the data set is {![]() }, where
}, where ![]() . Let
. Let ![]() , and let
, and let ![]() . The range of the variable is
. The range of the variable is ![]() .
.
The computations for the various binning methods are as follows:
-
For bucket binning, the length of the bucket is
![\[ L = \frac{\max (x) - \min (x)}{n} \]](images/prochp_hpbin0015.png)
The split points are
![\[ s_ k = \min (x) + L*k \]](images/prochp_hpbin0016.png)
where
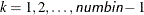 , and numbin is the value of the NUMBIN= option in the PROC HPBIN statement.
, and numbin is the value of the NUMBIN= option in the PROC HPBIN statement.
When the data are evenly distributed on the SAS appliance, the time complexity for bucket binning is
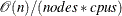 , where n is the number of observations,
, where n is the number of observations, 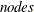 is the number of computer nodes on the appliance, and
is the number of computer nodes on the appliance, and 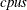 is the number of CPUs on each node.
is the number of CPUs on each node.
-
For quantile binning, PROC HPBIN calculates a quantile table
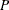 . Let
. Let 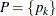 , where
, where 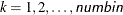 . Then
. Then 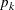 is described as
is described as
![\[ p_ k = \begin{cases} 1.0/\Argument{numbin} & \text { if } k = 0 \\ 1.0/\Argument{numbin} + p_{k-1} & \text { if } 0 < k < \Argument{numbin} \\ 1.0 & \text { if } k = \Argument{numbin} \\ \end{cases} \]](images/prochp_hpbin0025.png)
Quantile binning often requires data to be sorted in a particular way, and the sorting process usually consumes a significant amount of CPU time and memory. When the input data set is larger than the available memory, the sorting algorithm becomes more complicated. In distributed computing, data communications overhead also increases the sorting challenge. To avoid the time-consuming sorting process, the HPBIN procedure uses an iterative projection method for quantile binning, which runs much faster than sorting-based quantile binning method in most cases.
After calculating the quantile table, PROC HPBIN uses an iterative projection method to compute quantiles (percentiles) according to the formula that is described in the section Computing the Quantiles (Percentiles).
Quantile binning aims to assign the same number of observations to each bin, if the number of observations is evenly divisible by the number of bins. As a result, each bin should have the same number of observations, provided that there are no tied values at the boundaries of the bins. Because PROC HPBIN always assigns observations that have the same value to the same bin, quantile binning might create unbalanced bins if any variable has tied values. For example, if an observation whose value is x is assigned to bin k, then every observation whose value is x is assigned to bin k for this variable, and no observation whose value is x is assigned to the next bin, bin
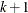 . Therefore, bin k might have more observations than bin
. Therefore, bin k might have more observations than bin 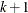 , because the tied values at the boundaries between bin k and bin
, because the tied values at the boundaries between bin k and bin 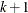 are all assigned to bin k. That is, tied values at the boundaries between two bins are always assigned to the lower-numbered bin.
are all assigned to bin k. That is, tied values at the boundaries between two bins are always assigned to the lower-numbered bin.
-
For pseudo–quantile binning and Winsorized binning, the sorting algorithm is more complex to describe but very efficient to execute. For variable x, PROC HPBIN uses a simple bucket sorting method to obtain the basic information. Let
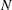 = 10,000 be the number of buckets, ranging from
= 10,000 be the number of buckets, ranging from 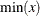 to
to 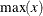 . For each bucket
. For each bucket 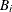 ,
, 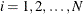 , PROC HPBIN keeps following information:
, PROC HPBIN keeps following information:
-
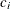 : count of x in
: count of x in 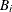
-
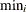 : minimum value of x in
: minimum value of x in 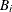
-
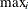 : maximum value of x in
: maximum value of x in 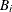
-
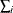 : sum of x in
: sum of x in 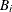
-
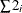 : sum of
: sum of 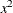 in
in 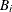
To calculate the quantile table, let
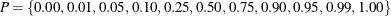 . For each
. For each 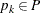 ,
, 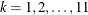 , find the smallest
, find the smallest 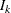 such that
such that 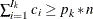 . Therefore, the quantile value
. Therefore, the quantile value 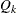 is obtained,
is obtained,
![\[ Q_ k= \begin{cases} min_{I_ k} & \text { if } \sum _{i=1}^{I_ k}{c_ i} > p_ k*n \\ max_{I_ k} & \text { if } \sum _{i=1}^{I_ k}{c_ i} = p_ k*n \end{cases} \]](images/prochp_hpbin0044.png)
where
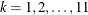 .
.
PROC HPBIN calculates the split points as follows:
-
-
For pseudo–quantile binning, let the base count
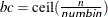 . PROC HPBIN finds those integers
. PROC HPBIN finds those integers 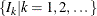 such that
such that
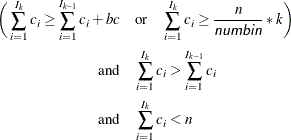
where k is the kth split.
The split value is
![\[ s_ k = \min (x) + \frac{\max (x) - \min (x)}{N}*I_ k \]](images/prochp_hpbin0048.png)
where
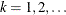 , and
, and 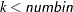 .
.
The time complexity for pseudo–quantile binning is
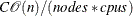 , where
, where 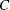 is a constant that depends on the number of sorting bucket
is a constant that depends on the number of sorting bucket 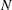 , n is the number of observations,
, n is the number of observations, 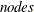 is the number of computer nodes on the appliance, and
is the number of computer nodes on the appliance, and 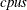 is the number of CPUs on each node.
is the number of CPUs on each node.
-
For Winsorized binning, the Winsorized statistics are computed first. After the minimum and maximum have been found, the split points are calculated the same way as in bucket binning.
Let the tail count
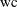 be
be 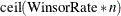 , and find the smallest
, and find the smallest 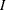 such that
such that 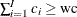 . Then, the left tail count is
. Then, the left tail count is 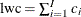 . Find the next
. Find the next 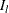 such that
such that 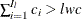 . Therefore, the minimum value is
. Therefore, the minimum value is 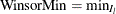 . Similarly, find the largest
. Similarly, find the largest 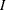 such that
such that 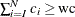 . The right tail count is
. The right tail count is 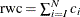 . Find the next
. Find the next 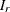 such that
such that 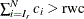 . Then the maximum value is
. Then the maximum value is 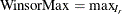 . The mean is calculated by the formula
. The mean is calculated by the formula
![\[ \mr{WinsorMean} = \frac{\mr{lwc} * \mr{WinsorMin} + \sum _{i=I_ l}^{I_ r}{sum_ i} + \mr{rwc} * \mr{WinsorMax} }{n} \]](images/prochp_hpbin0065.png)
The trimmed mean is calculated by the formula
![\[ \mr{trimmedMean} = \frac{\sum _{i=I_ l}^{I_ r}{sum_ i}}{n - \mr{lwc} - \mr{rwc}} \]](images/prochp_hpbin0066.png)
Note: PROC HPBIN prints an error or a warning message when the results might not be accurate.
Note: PROC HPBIN does not allow empty bins. If an empty bin is detected because of an insufficient number of nonmissing observations, PROC HPBIN issues an error and exits.
Note: If PROC HPBIN detects an empty bin followed by a bin that is not empty, it skips the empty bin and does not assign a number to it. In this case, the number of bins that PROC HPBIN generates is less than the specified number of bins.
