The HPDS2 Procedure

This example computes and plots a Mandelbrot set. The DS2 source statements that compute the set of coordinates that comprise the Mandelbrot set are submitted to the grid and executed alongside the database in distributed mode. Note that Mandelbrot set computation is perfectly scalable in that each point can be computed independently of every other point.

This example uses a DS2 procedure to create a data set that consists of one row for each Mandelbrot coordinate to be computed. The HPDS2 procedure reads this data set and computes the coordinates. The Mandelbrot set is then graphed by using the GCONTOUR procedure.

libname applianc &ENGINE
        server = "&GRIDDATASERVER"
        user   = &USER 
        password = &PASSWORD 
        database = &DATABASE;

/* Set up the table that contains one row for each coordinate to compute */
proc ds2;
   data inp(overwrite=yes);
      dcl double p q r;
      dcl integer maxiterate;
      method init();
         dcl int n m;
         dcl int i j k;
         dcl double pmin pmax qmin qmax;
         n = 1024;
         m = 1024;
         pmin = -1.5; pmax = -0.5;
         qmin = -0.5; qmax =  0.5;
         r = 100.0;
         maxiterate = 50;
         do k = 1 to n*m;
            i = k/m;
            j = mod(k,m);
            p = i*(pmax-pmin)/(n-1)+pmin;
            q = j*(qmax-qmin)/(m-1)+qmin;
            output;
         end;
      end;
   enddata;
run;
quit;

/* Compute the coordinates */
proc hpds2 data=inp out=applianc.mandelbrot;
   performance host="&GRIDHOST" install="&GRIDINSTALLLOC";
   data DS2GTF.out;
      dcl int mesh;
      dcl double x y rr nx ny;
      keep p q mesh;
      method run();
         set DS2GTF.in;
         x = p;
         y = q;
         rr = r**2;
         mesh = 0;
         do while (mesh < maxiterate and (x**2+y**2 < rr));
            nx = x**2 - y**2 + p;
            ny = 2.0*x*y + q;
            x = nx;
            y = ny;
            mesh = mesh+1;
         end;
      end;
   enddata;
run;

/* Plot the results */
goptions colors= (
CX003366 CX336699 CX6699CC CX99CCFF CX006633 CX339966 CX66CC99 CX99FFCC
CX336600 CX669933 CX99CC66 CXCCFF99 CX663300 CX996633 CXCC9966 CXFFCC99
CX660033 CX993366 CXCC6699 CXFF99CC CX003366 CX663399 CX9966CC CXCC99FF
CX003366 CX663399 CX9966CC CXCC99FF CX003366 CX663399 CX9966CC CXCC99FF
CX003366 CX663399 CX9966CC CXCC99FF CX003366 CX663399 CX9966CC CXCC99FF
black
)
;

proc gcontour data=applianc.mandelbrot;
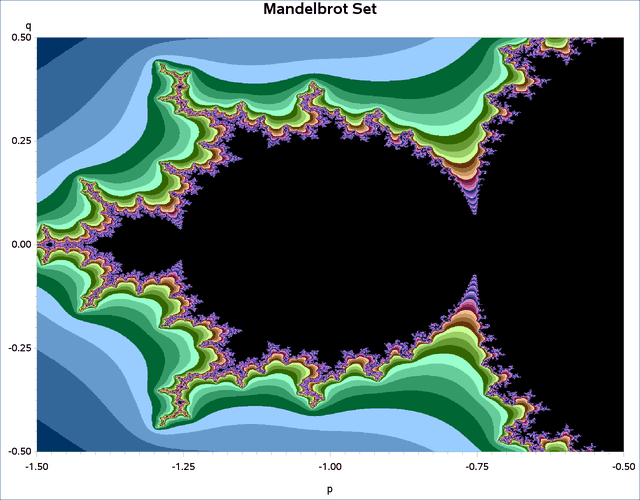
   Title 'Mandelbrot Set';
   plot q*p=mesh /
   nolegend
   pattern
   join
   levels = 5 to 45
  ;
run;

Output 7.1.1 shows the graphic representation of the Mandelbrot set that is computed by the HPDS2 procedure.