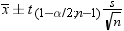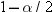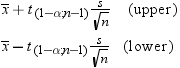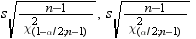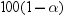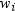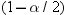MEANS Procedure
- Syntax

- Overview
- Concepts
- Using
- Results
- Examples
 Computing Specific Descriptive StatisticsComputing Descriptive Statistics with Class VariablesUsing the BY Statement with Class VariablesUsing a CLASSDATA= Data Set with Class VariablesUsing Multilabel Value Formats with Class VariablesUsing Preloaded Formats with Class VariablesComputing a Confidence Limit for the MeanComputing Output StatisticsComputing Different Output Statistics for Several VariablesComputing Output Statistics with Missing Class Variable ValuesIdentifying an Extreme Value with the Output StatisticsIdentifying the Top Three Extreme Values with the Output StatisticsUsing the STACKODSOUTPUT option to control data
Computing Specific Descriptive StatisticsComputing Descriptive Statistics with Class VariablesUsing the BY Statement with Class VariablesUsing a CLASSDATA= Data Set with Class VariablesUsing Multilabel Value Formats with Class VariablesUsing Preloaded Formats with Class VariablesComputing a Confidence Limit for the MeanComputing Output StatisticsComputing Different Output Statistics for Several VariablesComputing Output Statistics with Missing Class Variable ValuesIdentifying an Extreme Value with the Output StatisticsIdentifying the Top Three Extreme Values with the Output StatisticsUsing the STACKODSOUTPUT option to control data - References
Statistical Computations: MEANS Procedure
Computation of Moment Statistics
PROC
MEANS uses single-pass algorithms to compute the moment statistics
(such as mean, variance, skewness, and kurtosis). See Keywords and Formulas for the statistical
formulas.
Confidence Limits
With
the keywords CLM, LCLM, and UCLM, you can compute confidence limits
for the mean. A confidence limit is a range, constructed around the
value of a sample statistic, that contains the corresponding true
population value with given probability (ALPHA=) in repeated sampling.
where
 and
and  are the
are the  and
and 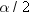 critical values of the chi-square statistic with
critical values of the chi-square statistic with
 degrees of freedom. A one-sided
degrees of freedom. A one-sided  % confidence interval is computed by replacing
% confidence interval is computed by replacing
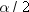 with
with  .
.
 and
and  are the
are the  and
and 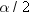 critical values of the chi-square statistic with
critical values of the chi-square statistic with
 degrees of freedom. A one-sided
degrees of freedom. A one-sided  % confidence interval is computed by replacing
% confidence interval is computed by replacing
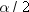 with
with  .
.
A  % confidence interval for the variance has upper
and lower limits that are equal to the squares of the corresponding
upper and lower limits for the standard deviation.
% confidence interval for the variance has upper
and lower limits that are equal to the squares of the corresponding
upper and lower limits for the standard deviation.
 % confidence interval for the variance has upper
and lower limits that are equal to the squares of the corresponding
upper and lower limits for the standard deviation.
% confidence interval for the variance has upper
and lower limits that are equal to the squares of the corresponding
upper and lower limits for the standard deviation.
Student's t Test
where  is the sample mean,
is the sample mean,  is the number of nonmissing values for a variable,
and
is the number of nonmissing values for a variable,
and  is the sample standard deviation. Under the null
hypothesis, the population mean equals
is the sample standard deviation. Under the null
hypothesis, the population mean equals 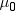 . When the data values are approximately normally
distributed, the probability under the null hypothesis of a t statistic
as extreme as, or more extreme than, the observed value (the p-value)
is obtained from the t distribution with
. When the data values are approximately normally
distributed, the probability under the null hypothesis of a t statistic
as extreme as, or more extreme than, the observed value (the p-value)
is obtained from the t distribution with  degrees of freedom. For large
degrees of freedom. For large  , the t statistic is asymptotically
equivalent to a z test.
, the t statistic is asymptotically
equivalent to a z test.
 is the sample mean,
is the sample mean,  is the number of nonmissing values for a variable,
and
is the number of nonmissing values for a variable,
and  is the sample standard deviation. Under the null
hypothesis, the population mean equals
is the sample standard deviation. Under the null
hypothesis, the population mean equals 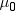 . When the data values are approximately normally
distributed, the probability under the null hypothesis of a t statistic
as extreme as, or more extreme than, the observed value (the p-value)
is obtained from the t distribution with
. When the data values are approximately normally
distributed, the probability under the null hypothesis of a t statistic
as extreme as, or more extreme than, the observed value (the p-value)
is obtained from the t distribution with  degrees of freedom. For large
degrees of freedom. For large  , the t statistic is asymptotically
equivalent to a z test.
, the t statistic is asymptotically
equivalent to a z test.
When you use the WEIGHT
statement or WEIGHT= in a VAR statement and the default value of VARDEF=,
which is DF, the Student's t statistic is calculated
as
where  is the weighted mean,
is the weighted mean,  is the weighted standard deviation, and
is the weighted standard deviation, and  is the weight for
is the weight for  observation. The
observation. The  statistic is treated as having a Student's t distribution
with
statistic is treated as having a Student's t distribution
with  degrees of freedom. If you specify the EXCLNPWGT
option in the PROC statement, then
degrees of freedom. If you specify the EXCLNPWGT
option in the PROC statement, then  is the number of nonmissing observations when the
value of the WEIGHT variable is positive. By default,
is the number of nonmissing observations when the
value of the WEIGHT variable is positive. By default,  is the number of nonmissing observations for the
WEIGHT variable.
is the number of nonmissing observations for the
WEIGHT variable.
 is the weighted mean,
is the weighted mean,  is the weighted standard deviation, and
is the weighted standard deviation, and  is the weight for
is the weight for  observation. The
observation. The  statistic is treated as having a Student's t distribution
with
statistic is treated as having a Student's t distribution
with  degrees of freedom. If you specify the EXCLNPWGT
option in the PROC statement, then
degrees of freedom. If you specify the EXCLNPWGT
option in the PROC statement, then  is the number of nonmissing observations when the
value of the WEIGHT variable is positive. By default,
is the number of nonmissing observations when the
value of the WEIGHT variable is positive. By default,  is the number of nonmissing observations for the
WEIGHT variable.
is the number of nonmissing observations for the
WEIGHT variable.
Quantiles
The options QMETHOD=, QNTLDEF=,
and QMARKERS= determine how PROC MEANS calculates quantiles. QNTLDEF=
deals with the mathematical definition of a quantile. See Quantile and Related Statistics. QMETHOD= deals with the mechanics of how PROC MEANS handles
the input data. The two methods are
If data set A has 100 unique values for a numeric
variable X and data set B has 1000 unique values for numeric variable
X, then QMETHOD=OS for data set B will take 10 times as much memory
as it does for data set A. If QMETHOD=P2, then both data sets A and
B will require the same memory space to generate quantiles.
The QMETHOD=P2 technique
is based on the piecewise-parabolic (P²) algorithm invented by
Jain and Chlamtac (1985). P² is a one-pass algorithm to determine
quantiles for a large data set. It requires a fixed amount of memory
for each variable for each level within the type. However, using simulation
studies, reliable estimations of some quantiles (P1, P5, P95, P99)
cannot be possible for some data sets such as data sets with heavily
tailed or skewed distributions.