The CPM Procedure

This example shows how you can schedule around holidays with PROC CPM. First, save a list of holidays in a SAS data set as SAS date variables. The length of the holidays is assumed to be measured in units specified by the INTERVAL= option. By default, all holidays are assumed to be one unit long. You can control the length of each holiday by specifying either the finish time for each holiday or the length of each holiday in the same observation as the holiday specification.

For example, the data set HOLIDAYS, displayed in Output 4.8.1 specifies two holidays, one for Christmas and the other for New Year’s Day. The variable holiday specifies the start of each holiday. The variable holifin specifies the end of the Christmas holiday as 26Dec03. Alternately, the variable holidur can be used to interpret the Christmas holiday as lasting four interval units starting from the 24th of December. If the variable holidur is used, the actual days when work is not done depends on the INTERVAL= option and on the underlying calendar used. This form of specifying holidays or breaks is useful for indicating vacations for specific employees. The second observation in the data set defines the New Year’s holiday as just one day long because both the variables holifin and holidur variables have missing values.

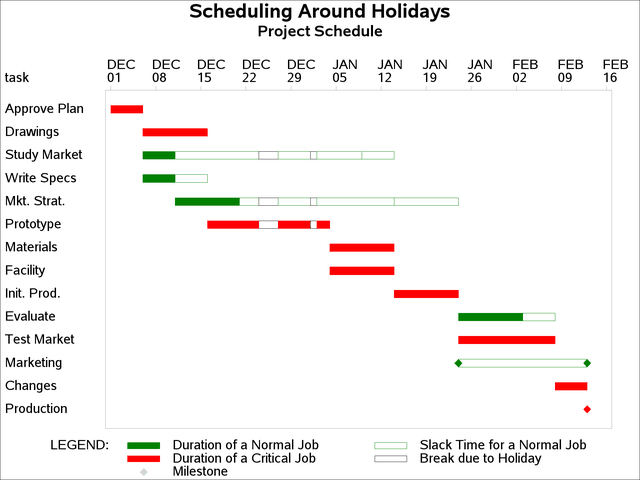
To invoke PROC CPM to schedule around holidays, use the HOLIDATA= option in the PROC CPM statement (see the following program) to identify the data set, and list the names of the variables in the data set in a HOLIDAY statement. The holiday start and finish are identified by specifying the HOLIDAY and HOLIFIN variables. Output 4.8.2 displays the schedule obtained.

proc cpm data=widget holidata=holidays
         out=saveh date='1dec03'd ;
   activity task;
   succ     succ1 succ2 succ3;
   duration days;
   holiday  holiday / holifin=(holifin);
   run;

proc sort data=saveh;
   by e_start;
   run;
pattern1 c=green v=s;     /* duration of a non-critical activity   */
pattern2 c=green v=e;     /* slack time for a noncrit. activity    */
pattern3 c=red   v=s;     /* duration of a critical activity       */
pattern4 c=magenta v=e;   /* slack time for a supercrit. activity  */
pattern5 c=magenta v=s;   /* duration of a supercrit. activity     */
pattern6 c=cyan v=s;      /* actual duration of an activity        */
pattern7 c=black v=e;     /* break due to a holiday                */

goptions vpos=50 hpos=80 border;
title 'Scheduling Around Holidays';
title2 'Project Schedule';

proc gantt graphics data=saveh holidata=holidays;
   chart / compress
           height=1.7 nojobnum skip=2
           dur=days increment=7
           holiday=(holiday) holifin=(holifin);

   id task;
   run;

Output 4.8.2: Scheduling around Holidays: Project Schedule

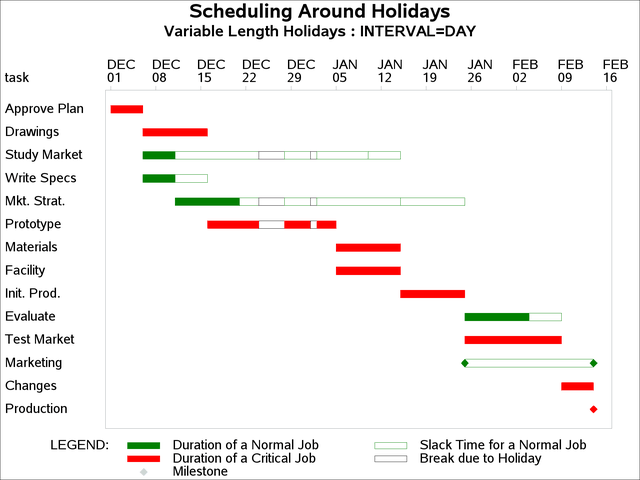
The next two invocations illustrate the use of the HOLIDUR= option and the effect of the INTERVAL= option on the duration of the holidays. Recall that the holiday duration is also assumed to be in interval units where interval is the value specified for the INTERVAL= option. Suppose that a holiday period for the entire project starts on December 24, 2003, with duration specified as 4. First the project is scheduled with INTERVAL=DAY so that the holidays are on December 24, 25, 26, and 27, 2003. Output 4.8.3 displays the resulting schedule. The project completion is delayed by one day due to the extra holiday on December 27, 2003.

proc cpm data=widget holidata=holidays
         out=saveh1 date='1dec03'd
         interval=day;
   activity task;
   succ     succ1 succ2 succ3;
   duration days;
   holiday  holiday / holidur=(holidur);
   run;

title2 'Variable Length Holidays : INTERVAL=DAY';
proc sort data=saveh1;
   by e_start;
   run;

proc gantt graphics data=saveh1 holidata=holidays;
   chart / compress
           height=1.7 skip=2
           nojobnum
           dur=days increment=7
           holiday=(holiday) holidur=(holidur) interval=day;

   id task;
   run;

Output 4.8.3: Scheduling around Holidays: INTERVAL=DAY

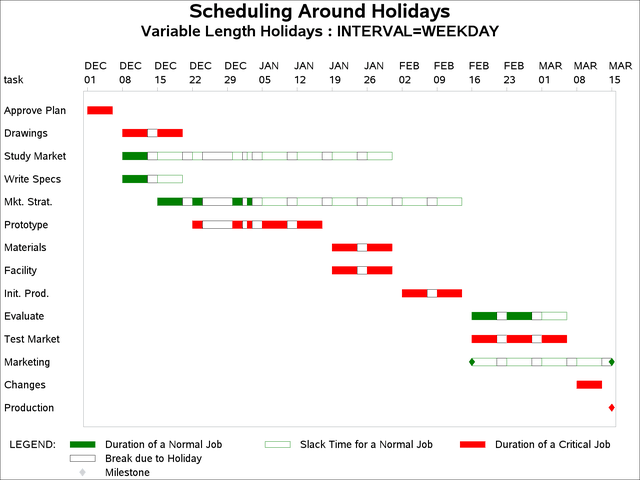
Next, suppose that work on the project is to be scheduled only on weekdays. The INTERVAL= option is set to WEEKDAY. Then, the value '4' specified for the variable holidur is interpreted as 4 weekdays. Thus, the holidays are on December 24, 25, 26, and 29, 2003, because December 27 and 28 (Saturday and Sunday) are non-working days anyway. (Note that if holifin had been used, the holiday would have ended on December 26, 2003.) The following statements schedule the project to start on December 1, 2003 with INTERVAL=WEEKDAY. Output 4.8.4 displays the resulting schedule. Note the further delay in project completion time.

proc cpm data=widget holidata=holidays
         out=saveh2 date='1dec03'd
         interval=weekday;
   activity task;
   succ     succ1 succ2 succ3;
   duration days;
   holiday  holiday / holidur=(holidur);
   run;

proc sort data=saveh2;
   by e_start;
   run;

title2 'Variable Length Holidays : INTERVAL=WEEKDAY';
proc gantt graphics data=saveh2 holidata=holidays;
   chart / compress
           height=1.8 skip=2
           nojobnum
           dur=days increment=7
           holiday=(holiday)
           holidur=(holidur)
           interval=weekday;

   id task;
   run;

Output 4.8.4: Scheduling around Holidays: INTERVAL=WEEKDAY

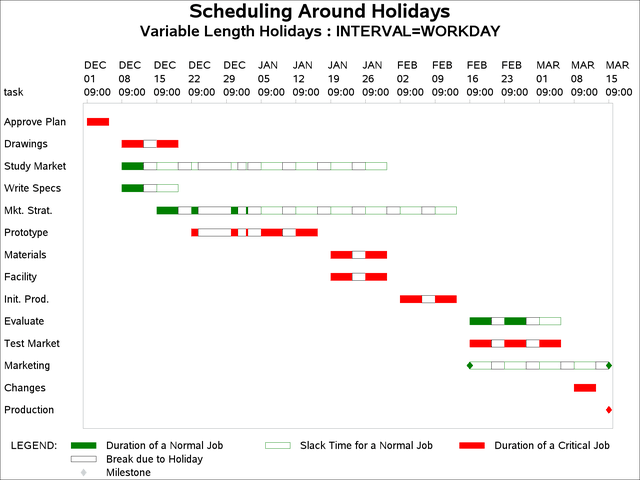
Finally, the same project is scheduled to start on December 1, 2003 with INTERVAL=WORKDAY. Output 4.8.5 displays the resulting Schedule data set. This time the holiday period starts at 5:00 p.m. on December 23, 2003, and ends at 9:00 a.m. on December 30, 2003.

proc cpm data=widget holidata=holidays
         out=saveh3 date='1dec03'd
         interval=workday;
   activity task;
   succ     succ1 succ2 succ3;
   duration days;
   holiday  holiday / holidur=(holidur);
   run;

proc sort data=saveh3;
   by e_start;
   run;

title2 'Variable Length Holidays : INTERVAL=WORKDAY';
proc gantt graphics data=saveh3 holidata=holidays;
   chart / compress
           height=1.8 nojobnum skip=2
           dur=days increment=7
           holiday=(holiday) holidur=(holidur) interval=workday;
   id task;
   run;

Output 4.8.5: Scheduling around Holidays: INTERVAL=WORKDAY