Introduction to Project Management: Subcontracting Decisions :: SAS/OR(R) 9.22 User's Guide: Project Management

Introduction to Project Management

Example 3.9 Subcontracting Decisions

Making decisions about subcontracting forms an important part of several medium-to-large scale projects. For example, in the pharmaceutical industry, the analysis of clinical trials may be a part of the drug development project that could either be accomplished by the company’s statistical group or be subcontracted to a statistical consulting firm. The decision may hinge upon how busy the local statistical group is with other projects that may delay the results of the analysis for the drug in question. Further, there may be more than one firm that is a likely candidate for performing the analysis. As a prerequisite for deciding whether to assign the analysis subproject to an external firm, you need to obtain a bid in the form of estimates of the cost and project duration from the competing firms as well as a corresponding estimate from the in-house team.

The cost corresponding to each possible subcontracting firm may be a combination of the actual costs (consulting fees and so on) and the tardiness of the project (tardiness being measured as the time difference between when the results are expected to be available and the target date for the availability of the results). The information required could be provided in terms of Gantt charts and cost analysis charts. Using this information, the project manager for the drug development project can use the principles of decision analysis to determine whether to do the analysis in-house or assign it to an outside consulting firm and to pick the firm to which the subcontract is to be assigned. Some of these ideas are illustrated in the following example.

Output 3.9.1 Input Data Sets for Decision Problem

Subcontracting Decision

The Stage Data Set

Obs	_STATE1	_STATE2	_VALUE_
1	On_Time	High	-12,000
2	On_Time	Low	-9,500
3	Delay	High	-15,000
4	Delay	Low	-11,500
5	Early		3,500
6	Late		1,500
7	Delay2		0

Subcontracting Decision

The Probability Data Set

Obs	_STATE1	_STATE2	_VALUE_
1	On_Time	High	-12,000
2	On_Time	Low	-9,500
3	Delay	High	-15,000
4	Delay	Low	-11,500
5	Early		3,500
6	Late		1,500
7	Delay2		0

Subcontracting Decision

The Payoffs Data Set

Obs	_STATE1	_STATE2	_VALUE_
1	On_Time	High	-12,000
2	On_Time	Low	-9,500
3	Delay	High	-15,000
4	Delay	Low	-11,500
5	Early		3,500
6	Late		1,500
7	Delay2		0

The stages of the decision problem are identified by the STAGEIN= data set, stage, displayed in Output 3.9.1. As a first step, the drug company needs to decide whether to perform the analysis in-house or to assign it to one of two consulting firms. If the in-house team is chosen, the resulting stage is a chance node, called 'Complete,' with two possible outcomes: 'On-Time' or 'Delay'; if there is a delay, the resulting cost to the drug company is 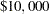$\text{[math]}$ . For each of these two outcomes, there is a second chance event corresponding to the cost of the analysis. For each of the two consulting firms, the outcome can be one of three possibilities: 'Early,' 'Late,' or 'Delay2'; if there is a delay, the drug company imposes a delay penalty of 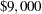$\text{[math]}$ on the firm, resulting in a net reward of 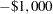$\text{[math]}$ (penalty of 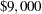$\text{[math]}$ minus the cost of $\text{[math]}$ ).

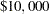The PROBIN= data set, prob, identifies the various probabilities associated with the different possible outcomes at each of the chance events. The prob data set is also displayed in Output 3.9.1.

The rewards (or payoffs) associated with each of the end stages are listed in the PAYOFFS= data set, payoff (also listed in Output 3.9.1). For example, for the in-house team, the high (low) cost associated with completing the analysis on time is 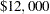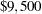$\text{[math]}$ ( $\text{[math]}$ ), and so on.

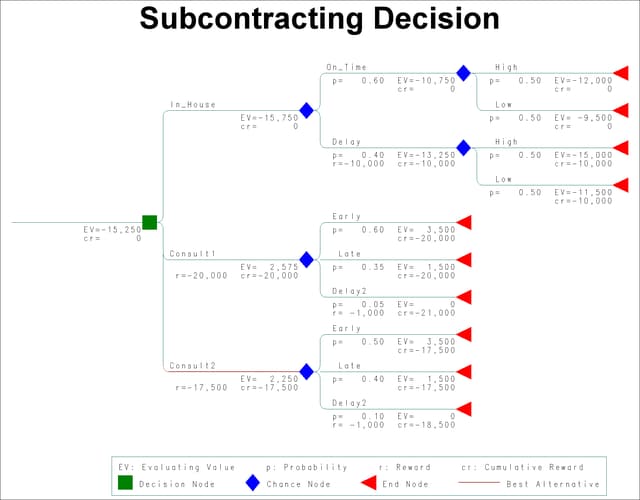
The following program invokes PROC DTREE to solve the decision problem. The complete decision tree, displayed in Output 3.9.2, represents the various stages and outcomes of the problem and identifies the optimal decision. In this example, the drug company should award the consulting contract to the second consulting firm as indicated by the red line for the corresponding branch of the tree.

See Chapter 5, The DTREE Procedure, for details about the DTREE procedure.

title "Subcontracting Decision";
symbol1 f=marker v=P c=blue;
symbol2 f=marker v=U c=green;
symbol3 f=marker v=A c=red;

 /* PROC DTREE statements */
proc dtree stagein=stage
           probin=prob
           payoffs=payoff
           nowarning
           ;
   evaluate;
   treeplot / graphics font='Cumberland AMT'
              compress ybetween=1 cell
              lwidth=1 lwidthb=2 hsymbol=2
              symbolc=1 symbold=2 symbole=3
              lstyleb=1
              ;
quit;

Output 3.9.2 Decision Analysis

Top of Page