| The DTREE Procedure |
Oil Wildcatter's Problem with Sounding Test
The wildcatter is impressed with the results of calculating
the values of perfect information and perfect control. After
comparing those values with the costs of the sounding test
and the cost-controlling procedure, he prefers to spend $![]() on
sounding test, which has a potential improvement of $
on
sounding test, which has a potential improvement of $![]() .
He is informed
that the sounding will disclose whether the terrain below has
no structure (which is bad), open structure (which is okay),
or closed structure (which is really hopeful). The expert also
provides him with the following table, which shows the conditional
probabilities.
.
He is informed
that the sounding will disclose whether the terrain below has
no structure (which is bad), open structure (which is okay),
or closed structure (which is really hopeful). The expert also
provides him with the following table, which shows the conditional
probabilities.
| Seismic Outcomes | |||
| State | No Structure | Open Structure | Closed Structure |
| Dry | 0.6 | 0.3 | 0.1 |
| Wet | 0.3 | 0.4 | 0.3 |
| Soaking | 0.1 | 0.4 | 0.5 |
To include this additional information into his basic problem,
the wildcatter needs to add two stages to his model: a decision
stage to represent the decision whether or not to take the
sounding test, and one chance stage to represent the uncertain
test result. The new STAGEIN=
data set is
/* -- create the STAGEIN= data set -- */
data Dtoils2;
format _STNAME_ $12. _STTYPE_ $2. _OUTCOM_ $14.
_SUCCES_ $12. _REWARD_ dollar12.0;
input _STNAME_ & _STTYPE_ & _OUTCOM_ &
_SUCCES_ & _REWARD_ dollar12.0;
datalines;
Drill D Drill Cost .
. . Not_Drill . .
Cost C Low Oil_Deposit .
. . Fair Oil_Deposit .
. . High Oil_Deposit .
Oil_Deposit C Dry . .
. . Wet . .
. . Soaking . .
Sounding D Noseismic Drill .
. . Seismic Structure -$60,000
Structure C No_Struct Drill .
. . Open_Struct Drill .
. . Closed_Struct Drill .
;
Note that the cost for the seismic soundings is represented as negative reward (of the outcome Seismic) in this data set. The conditional probabilities for stage Structure are added to the PROBIN= data set as follows:
/* -- create PROBIN= data set -- */
data Dtoilp2;
format _EVENT1 $10. _EVENT2 $12. _EVENT3 $14. ;
input _GIVEN_ $ _EVENT1 $ _PROB1
_EVENT2 $ _PROB2 _EVENT3 $ _PROB3;
datalines;
. Low 0.2 Fair 0.6 High 0.2
. Dry 0.5 Wet 0.3 Soaking 0.2
Dry No_Struct 0.6 Open_Struct 0.3 Closed_Struct 0.1
Wet No_Struct 0.3 Open_Struct 0.4 Closed_Struct 0.3
Soaking No_Struct 0.1 Open_Struct 0.4 Closed_Struct 0.5
;
It is not necessary to make any change to the PAYOFFS= data set. To evaluate his new model, the wildcatter invokes PROC DTREE as follows:
/* -- PROC DTREE statements -- */
title "Oil Wildcatter's Problem";
proc dtree stagein=Dtoils2
probin=Dtoilp2
payoffs=Dtoilu1
nowarning;
evaluate;
As before, the following messages are written to the SAS log:
NOTE: Present order of stages:
Sounding(D), Structure(C), Drill(D), Cost(C),
Oil_Deposit(C), _ENDST_(E).
NOTE: The currently optimal decision yields 140000.
The following SUMMARY statements produce optimal decision summary as shown in Figure 5.5 and Figure 5.6:
summary / target=Sounding;
summary / target=Drill;
The optimal strategy for the oil-drilling problem is found to be the following:
- No soundings test should be taken, and always drill. This
alternative has an expected payoff of $
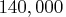 .
. - If the soundings test is conducted, then drill unless the test shows the terrain below has no structure.
- The soundings test is worth $
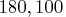 - $
- $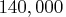 = $
= $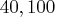 (this quantity is also called the value of imperfect
information or the value of sample information),
but it costs $
(this quantity is also called the value of imperfect
information or the value of sample information),
but it costs $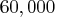 ; therefore, it should not be taken.
; therefore, it should not be taken.
Figure 5.5: Summary of the Oil Wildcatter's Problem for SOUNDING
The DTREE Procedure
Optimal Decision Summary
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figure 5.6: Summary of the Oil Wildcatter's Problem for DRILL
Note that the value of sample information also can be obtained by using the following statements:
modify Seismic reward 0;
evaluate;
The following messages, which appear in the SAS log, show the expected
payoff with soundings test is $![]() . Recall that the expected
value without test information is $
. Recall that the expected
value without test information is $![]() . Again, following the
previous calculation, the value of test information is
$
. Again, following the
previous calculation, the value of test information is
$![]() - $
- $![]() = $
= $![]() .
.
NOTE: The reward of outcome Seismic has been changed to 0.
NOTE: The currently optimal decision yields 180100.
Now, the wildcatter has the information to make his best decision.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.