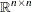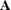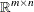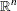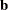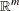The Quadratic Programming Solver

Overview: QP Solver

The OPTMODEL procedure provides a framework for specifying and solving quadratic programs.

Mathematically, a quadratic programming (QP) problem can be stated as follows:

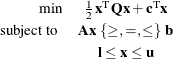
$\begin{eqnarray*} \min & \frac{1}{2}\, \mathbf{x}^\textrm {T} \mathbf{Qx} + \mathbf{c}^\textrm {T} \mathbf{x} \\ \mbox{subject to } & \mathbf{A x} \; \{ \ge , =, \le \} \; \mathbf{b} \\ & \mathbf{l} \le \mathbf{x} \le \mathbf{u} \end{eqnarray*}$

where

$\mathbf{Q}$	$\in$	$\mathbb {R}^{n\times n}$	is the quadratic (also known as Hessian) matrix
$\mathbf{A}$	$\in$	$\mathbb {R}^{m\times n}$	is the constraints matrix
$\mathbf{x}$	$\in$	$\mathbb {R}^{n}$	is the vector of decision variables
$\mathbf{c}$	$\in$	$\mathbb {R}^{n}$	is the vector of linear objective function coefficients
$\mathbf{b}$	$\in$	$\mathbb {R}^{m}$	is the vector of constraints right-hand sides (RHS)
$\mathbf{l}$	$\in$	$\mathbb {R}^{n}$	is the vector of lower bounds on the decision variables
$\mathbf{u}$	$\in$	$\mathbb {R}^{n}$	is the vector of upper bounds on the decision variables

The quadratic matrix 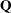$\mathbf{Q}$ is assumed to be symmetric; that is,

$q_{ij} = q_{ji},\quad \forall i,j = 1, \ldots , n$

Indeed, it is easy to show that even if 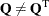$\mathbf{Q} \not= \mathbf{Q}^\mr {T}$ , then the simple modification

$\tilde{\mathbf{Q}} = \frac{1}{2}(\mathbf{Q} + \mathbf{Q}^\textrm {T})$

produces an equivalent formulation 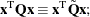$\mathbf{x}^\mr {T}\mathbf{Qx} \equiv \mathbf{x}^\mr {T} \tilde{\mathbf{Q}}\mathbf{x};$ hence symmetry is assumed. When you specify a quadratic matrix, it suffices to list only lower triangular coefficients.

In addition to being symmetric, 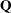$\mathbf{Q}$ is also required to be positive semidefinite for minimization type of models:

$\mathbf{x}^\textrm {T}\mathbf{Qx} \ge 0,\quad \forall \mathbf{x}\in \mathbb {R}^ n$

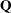$\mathbf{Q}$ is required to be negative semidefinite for maximization type of models. Convexity can come as a result of a matrix-matrix multiplication

$\mathbf{Q} = \mathbf{L}\mathbf{L}^\textrm {T}$

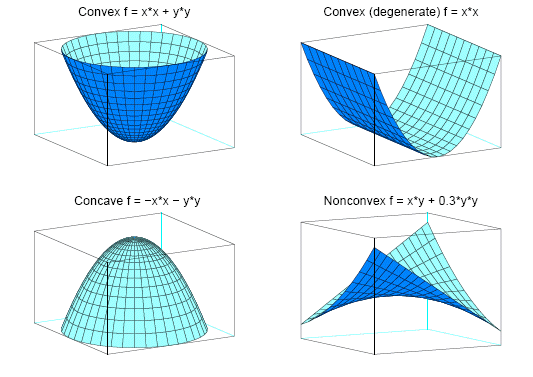
or as a consequence of physical laws, and so on. See Figure 11.1 for examples of convex, concave, and nonconvex objective functions.

Figure 11.1: Examples of Convex, Concave, and Nonconvex Objective Functions

The order of constraints is insignificant. Some or all components of $\mathbf{l}$ or $\mathbf{u}$ (lower and upper bounds, respectively) can be omitted.