The Mixed Integer Linear Programming Solver
The traveling salesman problem (TSP) is that of finding a minimum cost tour in an undirected graph G with vertex set ![]() and edge set E. A tour is a connected subgraph for which each vertex has degree two. The goal is then to find a tour of minimum total cost,
where the total cost is the sum of the costs of the edges in the tour. With each edge
and edge set E. A tour is a connected subgraph for which each vertex has degree two. The goal is then to find a tour of minimum total cost,
where the total cost is the sum of the costs of the edges in the tour. With each edge ![]() we associate a binary variable
we associate a binary variable ![]() , which indicates whether edge e is part of the tour, and a cost
, which indicates whether edge e is part of the tour, and a cost ![]() . Let
. Let ![]() . Then an integer linear programming (ILP) formulation of the TSP is as follows:
. Then an integer linear programming (ILP) formulation of the TSP is as follows:
![\[ \begin{array}{llllll} \min & \displaystyle \sum _{e \in E} c_ e x_ e \\ \mr{s.t.} & \displaystyle \sum _{e \in \delta ({i})}x_ e & = & 2 & \forall i \in V & (\mr{two\_ match}) \\ & \displaystyle \sum _{e \in \delta (S)}x_ e & \geq & 2 & \forall S \subset V, \; 2 \leq |S| \leq |V| - 1 & (\mr{subtour\_ elim})\\ & x_ e \in \{ 0,1\} & & & \forall e \in E \end{array} \]](images/ormpug_milpsolver0089.png)
The equations (two_match) are the matching constraints, which ensure that each vertex has degree two in the subgraph, while the inequalities (subtour_elim) are known as the subtour elimination constraints (SECs) and enforce connectivity.
Since there is an exponential number ![]() of SECs, it is impossible to explicitly construct the full TSP formulation for large graphs. An alternative formulation of
polynomial size was introduced by Miller, Tucker, and Zemlin (1960) (MTZ):
of SECs, it is impossible to explicitly construct the full TSP formulation for large graphs. An alternative formulation of
polynomial size was introduced by Miller, Tucker, and Zemlin (1960) (MTZ):
![\[ \begin{array}{llllll} \min & \displaystyle \sum _{(i,j) \in E} c_{ij} x_{ij} \\ \mr{s.t.} & \displaystyle \sum _{j \in V} x_{ij} & = & 1 & \forall i \in V & \mr{(assign\_ i)} \\ & \displaystyle \sum _{i \in V} x_{ij} & = & 1 & \forall j \in V & \mr{(assign\_ j)} \\ & u_ i - u_ j + 1 & \leq & (|V|-1)(1-x_{ij}) & \forall (i,j) \in V, i \neq 1, j \neq 1 & \mr{(mtz)}\\ & 2 \leq u_{i} & \leq & |V| & \forall i \in \{ 2,..,|V|\} , \\ & x_{ij} \in \{ 0,1\} & & & \forall (i,j) \in E \end{array} \]](images/ormpug_milpsolver0091.png)
This formulation uses a directed graph. Constraints (assign_i) and (assign_j) now enforce that each vertex has degree two (one edge in, one edge out). The MTZ constraints (mtz) enforce that no subtours exist.
TSPLIB, located at http://elib.zib.de/pub/Packages/mp-testdata/tsp/tsplib/tsplib.html, is a set of benchmark instances for the TSP. The following DATA step converts a TSPLIB instance of type EUC_2D into a SAS data set that contains the coordinates of the vertices:
/* convert the TSPLIB instance into a data set */
data tspData(drop=H);
infile "st70.tsp";
input H $1. @;
if H not in ('N','T','C','D','E');
input @1 var1-var3;
run;
The following PROC OPTMODEL statements attempt to solve the TSPLIB instance st70.tsp by using the MTZ formulation:
/* direct solution using the MTZ formulation */
proc optmodel;
set VERTICES;
set EDGES = {i in VERTICES, j in VERTICES: i ne j};
num xc {VERTICES};
num yc {VERTICES};
/* read in the instance and customer coordinates (xc, yc) */
read data tspData into VERTICES=[_n_] xc=var2 yc=var3;
/* the cost is the euclidean distance rounded to the nearest integer */
num c {<i,j> in EDGES}
init floor( sqrt( ((xc[i]-xc[j])**2 + (yc[i]-yc[j])**2)) + 0.5);
var x {EDGES} binary;
var u {i in 2..card(VERTICES)} >= 2 <= card(VERTICES);
/* each vertex has exactly one in-edge and one out-edge */
con assign_i {i in VERTICES}:
sum {j in VERTICES: i ne j} x[i,j] = 1;
con assign_j {j in VERTICES}:
sum {i in VERTICES: i ne j} x[i,j] = 1;
/* minimize the total cost */
min obj
= sum {<i,j> in EDGES} (if i > j then c[i,j] else c[j,i]) * x[i,j];
/* no subtours */
con mtz {<i,j> in EDGES : (i ne 1) and (j ne 1)}:
u[i] - u[j] + 1 <= (card(VERTICES) - 1) * (1 - x[i,j]);
solve with milp / maxtime = 600;
quit;
It is well known that the MTZ formulation is much weaker than the subtour formulation. The exponential number of SECs makes it impossible, at least in large instances, to use a direct call to the MILP solver with the subtour formulation. For this reason, if you want to solve the TSP with one SOLVE statement, you must use the MTZ formulation and rely strictly on generic cuts and heuristics. Except for very small instances, this is unlikely to be a good approach.
A much more efficient way to tackle the TSP is to dynamically generate the subtour inequalities as cuts. Typically this is done by solving the LP relaxation of the two-matching problem, finding violated subtour cuts, and adding them iteratively. The problem of finding violated cuts is known as the separation problem. In this case, the separation problem takes the form of a minimum cut problem, which is nontrivial to implement efficiently. Therefore, for the sake of illustration, an integer program is solved at each step of the process.
The initial formulation of the TSP is the integral two-matching problem. You solve this by using PROC OPTMODEL to obtain an integral matching, which is not necessarily a tour. In this case, the separation problem is trivial. If the solution is a connected graph, then it is a tour, so the problem is solved. If the solution is a disconnected graph, then each component forms a violated subtour constraint. These constraints are added to the formulation, and the integer program is solved again. This process is repeated until the solution defines a tour.
The following PROC OPTMODEL statements solve the TSP by using the subtour formulation and iteratively adding subtour constraints:
/* iterative solution using the subtour formulation */
proc optmodel;
set VERTICES;
set EDGES = {i in VERTICES, j in VERTICES: i > j};
num xc {VERTICES};
num yc {VERTICES};
num numsubtour init 0;
set SUBTOUR {1..numsubtour};
/* read in the instance and customer coordinates (xc, yc) */
read data tspData into VERTICES=[var1] xc=var2 yc=var3;
/* the cost is the euclidean distance rounded to the nearest integer */
num c {<i,j> in EDGES}
init floor( sqrt( ((xc[i]-xc[j])**2 + (yc[i]-yc[j])**2)) + 0.5);
var x {EDGES} binary;
/* minimize the total cost */
min obj =
sum {<i,j> in EDGES} c[i,j] * x[i,j];
/* each vertex has exactly one in-edge and one out-edge */
con two_match {i in VERTICES}:
sum {j in VERTICES: i > j} x[i,j]
+ sum {j in VERTICES: i < j} x[j,i] = 2;
/* no subtours (these constraints are generated dynamically) */
con subtour_elim {s in 1..numsubtour}:
sum {<i,j> in EDGES: (i in SUBTOUR[s] and j not in SUBTOUR[s])
or (i not in SUBTOUR[s] and j in SUBTOUR[s])} x[i,j] >= 2;
/* this starts the algorithm to find violated subtours */
set <num,num> EDGES1;
set INITVERTICES = setof{<i,j> in EDGES1} i;
set VERTICES1;
set NEIGHBORS;
set <num,num> CLOSURE;
num component {INITVERTICES};
num numcomp init 2;
num iter init 1;
num numiters init 1;
set ITERS = 1..numiters;
num sol {ITERS, EDGES};
/* initial solve with just matching constraints */
solve;
call symput(compress('obj'||put(iter,best.)),
trim(left(put(round(obj),best.))));
for {<i,j> in EDGES} sol[iter,i,j] = round(x[i,j]);
/* while the solution is disconnected, continue */
do while (numcomp > 1);
iter = iter + 1;
/* find connected components of support graph */
EDGES1 = {<i,j> in EDGES: round(x[i,j].sol) = 1};
EDGES1 = EDGES1 union {setof {<i,j> in EDGES1} <j,i>};
VERTICES1 = INITVERTICES;
CLOSURE = EDGES1;
for {i in INITVERTICES} component[i] = 0;
for {i in VERTICES1} do;
NEIGHBORS = slice(<i,*>,CLOSURE);
CLOSURE = CLOSURE union (NEIGHBORS cross NEIGHBORS);
end;
numcomp = 0;
do while (card(VERTICES1) > 0);
numcomp = numcomp + 1;
for {i in VERTICES1} do;
NEIGHBORS = slice(<i,*>,CLOSURE);
for {j in NEIGHBORS} component[j] = numcomp;
VERTICES1 = VERTICES1 diff NEIGHBORS;
leave;
end;
end;
if numcomp = 1 then leave;
numiters = iter;
numsubtour = numsubtour + numcomp;
for {comp in 1..numcomp} do;
SUBTOUR[numsubtour-numcomp+comp]
= {i in VERTICES: component[i] = comp};
end;
solve;
call symput(compress('obj'||put(iter,best.)),
trim(left(put(round(obj),best.))));
for {<i,j> in EDGES} sol[iter,i,j] = round(x[i,j]);
end;
/* create a data set for use by gplot */
create data solData from
[iter i j]={it in ITERS, <i,j> in EDGES: sol[it,i,j] = 1}
xi=xc[i] yi=yc[i] xj=xc[j] yj=yc[j];
call symput('numiters',put(numiters,best.));
quit;
You can generate plots of the solution and objective value at each stage by using the following statements:
%macro plotTSP;
%annomac;
%do i = 1 %to &numiters;
/* create annotate data set to draw subtours */
data anno(drop=iter xi yi xj yj);
%SYSTEM(2, 2, 2);
set solData(keep=iter xi yi xj yj);
where iter = &i;
%LINE(xi, yi, xj, yj, *, 1, 1);
run;
title1 h=2 "TSP: Iter = &i, Objective = &&obj&i";
title2;
proc gplot data=tspData anno=anno;
axis1 label=none;
symbol1 value=dot interpol=none
pointlabel=("#var1" nodropcollisions height=1) cv=black;
plot var3*var2 / haxis=axis1 vaxis=axis1;
run;
quit;
%end;
%mend plotTSP;
%plotTSP;
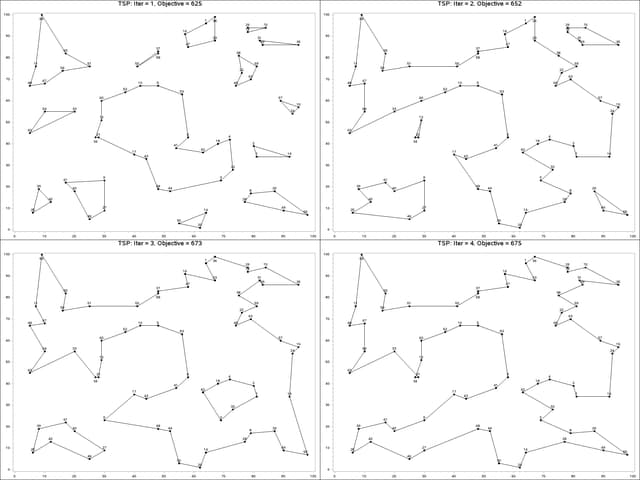
The plot in Output 8.4.1 shows the solution and objective value at each stage. Notice that each stage restricts some subset of subtours. When you reach the final stage, you have a valid tour.
Note: An alternative way of approaching the TSP is to use a genetic algorithm. See the "Examples" section in Chapter 4: The GA Procedure in SAS/OR 13.2 User's Guide: Local Search Optimization, for an example of how to use PROC GA to solve the TSP.
Note: See the "Examples" section in Chapter 2: The OPTNET Procedure in SAS/OR 13.2 User's Guide: Network Optimization Algorithms, for an example of how to use PROC OPTNET to solve the TSP.