The OPTQP Procedure
The interior point solver in PROC OPTQP implements an infeasible primal-dual predictor-corrector interior point algorithm. To illustrate the algorithm and the concepts of duality and dual infeasibility, consider the following QP formulation (the primal):
The corresponding dual is as follows:
![\[ \begin{array}{rccccccl} \mbox{max} & - \frac{1}{2}\mathbf{x}^\mr {T}\mathbf{Qx} & + & \mathbf{b}^\mr {T} \mathbf{y} & & & & \\ \mbox{subject to} & -\mathbf{Qx} & + & \mathbf{A}^\mr {T} \mathbf{y} & + & \mathbf{w} & = & \mathbf{c} \\ & & & & & \mathbf{y} & \ge & \mathbf{0} \\ & & & & & \mathbf{w} & \ge & \mathbf{0} \end{array} \]](images/ormpug_optqp0043.png)
where ![]() refers to the vector of dual variables and
refers to the vector of dual variables and ![]() refers to the vector of slack variables in the dual problem.
refers to the vector of slack variables in the dual problem.
The dual makes an important contribution to the certificate of optimality for the primal. The primal and dual constraints combined with complementarity conditions define the first-order optimality conditions, also known as KKT (Karush-Kuhn-Tucker) conditions, which can be stated as follows:
![\[ \begin{array}{rclr} \mathbf{A}\mathbf{x} - \mathbf{s} & = & \mathbf{b} & \mr {(primal~ feasibility)} \\ -\mathbf{Qx} + \mathbf{A}^\mr {T} \mathbf{y} + \mathbf{w} & = & \mathbf{c} & \mr {(dual~ feasibility)}\\ \mathbf{W} \mathbf{X} \mathbf{e} & = & \mathbf{0} & \mr {(complementarity)}\\ \mathbf{S} \mathbf{Y} \mathbf{e} & = & \mathbf{0} & \mr {(complementarity)}\\ \mathbf{x},\, \mathbf{y},\, \mathbf{w}, \, \mathbf{s} & \ge & \mathbf{0} & \\ \end{array} \]](images/ormpug_optqp0046.png)
where ![]() is of appropriate dimension and
is of appropriate dimension and ![]() is the vector of primal slack variables.
is the vector of primal slack variables.
Note: Slack variables (the s vector) are automatically introduced by the solver when necessary; it is therefore recommended that you not introduce any slack variables explicitly. This enables the solver to handle slack variables much more efficiently.
The letters ![]()
![]()
![]() and
and ![]() denote matrices with corresponding x, y, w, and s on the main diagonal and zero elsewhere, as in the following example:
denote matrices with corresponding x, y, w, and s on the main diagonal and zero elsewhere, as in the following example:
![\[ \mathbf{X} \equiv \left[ \begin{array}{cccc} x_1 & 0 & \cdots & 0 \\ 0 & x_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & x_ n \end{array} \right] \]](images/ormpug_optqp0053.png)
If ![]() is a solution of the previously defined system of equations that represent the KKT conditions, then
is a solution of the previously defined system of equations that represent the KKT conditions, then ![]() is also an optimal solution to the original QP model.
is also an optimal solution to the original QP model.
At each iteration the interior point algorithm solves a large, sparse system of linear equations as follows:
where ![]() and
and ![]() denote the vector of search directions in the primal and dual spaces, respectively, and
denote the vector of search directions in the primal and dual spaces, respectively, and ![]() and
and ![]() constitute the vector of the right-hand sides.
constitute the vector of the right-hand sides.
The preceding system is known as the reduced KKT system. PROC OPTQP uses a preconditioned quasi-minimum residual algorithm to solve this system of equations efficiently.
An important feature of the interior point solver is that it takes full advantage of the sparsity in the constraint and quadratic matrices, thereby enabling it to efficiently solve large-scale quadratic programs.
The interior point algorithm works simultaneously in the primal and dual spaces. It attains optimality when both primal and
dual feasibility are achieved and when complementarity conditions hold. Therefore, it is of interest to observe the following
four measures where ![]() is the Euclidean norm of the vector v:
is the Euclidean norm of the vector v:
-
relative primal infeasibility measure
 :
:
![\[ \alpha = \frac{\| \mathbf{Ax} - \mathbf{b} - \mathbf{s}\| _2}{\| \mathbf{b}\| _2 + 1} \]](images/ormpug_optqp0062.png)
-
relative dual infeasibility measure
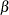 :
:
![\[ \beta = \frac{\| \mathbf{Qx} + \mathbf{c} - \mathbf{A}^\textrm {T} \mathbf{y} - \mathbf{w} \| _2}{\| \mathbf{c}\| _2 + 1} \]](images/ormpug_optqp0063.png)
-
relative duality gap
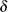 :
:
![\[ \delta = \frac{|\mathbf{x}^\textrm {T}\mathbf{Qx}+\mathbf{c}^\textrm {T}\mathbf{x} - \mathbf{b}^\textrm {T}\mathbf{y}|}{|\frac{1}{2}\mathbf{x}^\textrm {T}\mathbf{Qx}+\mathbf{c}^\textrm {T}\mathbf{x}| + 1} \]](images/ormpug_optqp0064.png)
-
absolute complementarity
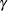 :
:
![\[ \gamma =\sum _{i=1}^ n x_ iw_ i + \sum _{i=1}^ m y_ i s_ i \]](images/ormpug_optqp0066.png)
These measures are displayed in the iteration log.
