The OPTLP Procedure

Example 10.8 Using the Network Simplex Solver

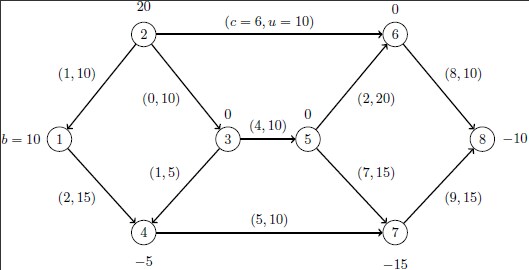
This example demonstrates how to use the network simplex solver to find the minimum-cost flow in a directed graph. Consider the directed graph in Output 10.8.1, which appears in Ahuja, Magnanti, and Orlin (1993).

Output 10.8.1: Minimum Cost Network Flow Problem: Data

You can use the following SAS statements to create the input data set ex8:

data ex8;
   input field1 $8. field2 $13. @25 field3 $13. field4  @53 field5 $13. field6;
   datalines;
NAME    .               .                    .      .                   .
ROWS    .               .                    .      .                   .
N       obj             .                    .      .                   .
E       balance['1']    .                    .      .                   .
E       balance['2']    .                    .      .                   .
E       balance['3']    .                    .      .                   .
E       balance['4']    .                    .      .                   .
E       balance['5']    .                    .      .                   .
E       balance['6']    .                    .      .                   .
E       balance['7']    .                    .      .                   .
E       balance['8']    .                    .      .                   .
COLUMNS .               .                    .      .                   .
.       x['1','4']      obj                  2      balance['1']        1
.       x['1','4']      balance['4']        -1      .                   .
.       x['2','1']      obj                  1      balance['1']       -1
.       x['2','1']      balance['2']         1      .                   .
.       x['2','3']      balance['2']         1      balance['3']       -1
.       x['2','6']      obj                  6      balance['2']        1
.       x['2','6']      balance['6']        -1      .                   .
.       x['3','4']      obj                  1      balance['3']        1
.       x['3','4']      balance['4']        -1      .                   .
.       x['3','5']      obj                  4      balance['3']        1
.       x['3','5']      balance['5']        -1      .                   .
.       x['4','7']      obj                  5      balance['4']        1
.       x['4','7']      balance['7']        -1      .                   .
.       x['5','6']      obj                  2      balance['5']        1
.       x['5','6']      balance['6']        -1      .                   .
.       x['5','7']      obj                  7      balance['5']        1
.       x['5','7']      balance['7']        -1      .                   .
.       x['6','8']      obj                  8      balance['6']        1
.       x['6','8']      balance['8']        -1      .                   .
.       x['7','8']      obj                  9      balance['7']        1
.       x['7','8']      balance['8']        -1      .                   .
RHS     .               .                    .      .                   .
.       .RHS.           balance['1']        10      .                   .
.       .RHS.           balance['2']        20      .                   .
.       .RHS.           balance['4']        -5      .                   .
.       .RHS.           balance['7']       -15      .                   .
.       .RHS.           balance['8']       -10      .                   .
BOUNDS  .               .                    .      .                   .
UP      .BOUNDS.        x['1','4']          15      .                   .
UP      .BOUNDS.        x['2','1']          10      .                   .
UP      .BOUNDS.        x['2','3']          10      .                   .
UP      .BOUNDS.        x['2','6']          10      .                   .
UP      .BOUNDS.        x['3','4']           5      .                   .
UP      .BOUNDS.        x['3','5']          10      .                   .
UP      .BOUNDS.        x['4','7']          10      .                   .
UP      .BOUNDS.        x['5','6']          20      .                   .
UP      .BOUNDS.        x['5','7']          15      .                   .
UP      .BOUNDS.        x['6','8']          10      .                   .
UP      .BOUNDS.        x['7','8']          15      .                   .
ENDATA  .               .                    .      .                   .
;

You can use the following call to PROC OPTLP to find the minimum-cost flow:

proc optlp
  presolver  = none
  printlevel = 2
  logfreq    = 1
  data       = ex8
  primalout  = ex8out
  algorithm  = ns;
run;

The optimal solution is displayed in Output 10.8.2.

Output 10.8.2: Network Simplex Solver: Primal Solution Output

Primal Solution

Obs	Objective Function ID	RHS ID	Variable Name	Variable Type	Objective Coefficient	Upper Bound	Variable Value	Variable Status	Reduced Cost
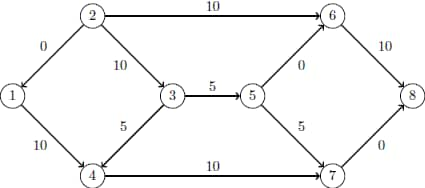
1	obj	.RHS.	x['1','4']	D	2	15	10	B	0
2	obj	.RHS.	x['2','1']	D	1	10	0	L	2
3	obj	.RHS.	x['2','3']	D	0	10	10	B	0
4	obj	.RHS.	x['2','6']	D	6	10	10	B	0
5	obj	.RHS.	x['3','4']	D	1	5	5	B	0
6	obj	.RHS.	x['3','5']	D	4	10	5	B	0
7	obj	.RHS.	x['4','7']	D	5	10	10	U	-5
8	obj	.RHS.	x['5','6']	D	2	20	0	L	0
9	obj	.RHS.	x['5','7']	D	7	15	5	B	0
10	obj	.RHS.	x['6','8']	D	8	10	10	B	0
11	obj	.RHS.	x['7','8']	D	9	15	0	L	6

The optimal solution is represented graphically in Output 10.8.3.

Output 10.8.3: Minimum Cost Network Flow Problem: Optimal Solution

The iteration log is displayed in Output 10.8.4.

Output 10.8.4: Log: Solution Progress

NOTE: The problem has 11 variables (0 free, 0 fixed).

NOTE: The problem has 8 constraints (0 LE, 8 EQ, 0 GE, 0 range).

NOTE: The problem has 22 constraint coefficients.

NOTE: The LP presolver value NONE is applied.

NOTE: The LP solver is called.

NOTE: The Network Simplex algorithm is used.

NOTE: The network has 8 rows (100.00%), 11 columns (100.00%), and 1 component.

NOTE: The network extraction and setup time is 0.00 seconds.

Primal Primal Dual

Iteration Objective Infeasibility Infeasibility Time

1 0 20.0000000 89.0000000 0.00

2 0 20.0000000 89.0000000 0.00

3 5.0000000 15.0000000 84.0000000 0.00

4 5.0000000 15.0000000 83.0000000 0.00

5 75.0000000 15.0000000 83.0000000 0.00

6 75.0000000 15.0000000 79.0000000 0.00

7 130.0000000 10.0000000 76.0000000 0.00

8 270.0000000 0 0 0.00

NOTE: The Network Simplex solve time is 0.00 seconds.

NOTE: The total Network Simplex solve time is 0.00 seconds.

NOTE: Optimal.

NOTE: Objective = 270.

NOTE: The data set WORK.EX8OUT has 11 observations and 10 variables.