MILP Solver Options :: SAS/OR(R) 12.3 User's Guide: Mathematical Programming

Presolve Option

PRESOLVER=number | string

specifies a presolve string or its corresponding value number, as listed in Table 7.2.

Table 7.2: Values for PRESOLVER= Option

number	string	Description
–1	AUTOMATIC	Applies the default level of presolve processing
0	NONE	Disables presolver
1	BASIC	Performs minimal presolve processing
2	MODERATE	Applies a higher level of presolve processing
3	AGGRESSIVE	Applies the highest level of presolve processing

The default value is AUTOMATIC.

Warm Start Option

PRIMALIN

enables you to input a starting solution in PROC OPTMODEL before invoking the MILP solver. Adding the PRIMALIN option to the SOLVE statement requests that the MILP solver use the current variable values as a starting solution (warm start). If the MILP solver finds that the input solution is feasible, then the input solution provides an incumbent solution and a bound for the branch-and-bound algorithm. If the solution is not feasible, the MILP solver tries to repair it. It is possible to set a variable value to the missing value '.' to mark a variable for repair. When it is difficult to find a good integer feasible solution for a problem, warm start can reduce solution time significantly.

Note: If the MILP solver produces a feasible solution, the variable values from that run can be used as the warm start solution for a subsequent run. If the warm start solution is not feasible for the subsequent run, the solver automatically tries to repair it.

Control Options

ABSOBJGAP=number

specifies a stopping criterion. When the absolute difference between the best integer objective and the objective of the best remaining node falls below the value of number, the solver stops. The value of number can be any nonnegative number; the default value is 1E–6.

CUTOFF=number

cuts off any nodes in a minimization (maximization) problem with an objective value above (below) number. The value of number can be any number; the default value is the positive (negative) number that has the largest absolute value representable in your operating environment.

EMPHASIS=number | string

specifies a search emphasis string or its corresponding value number as listed in Table 7.3.

Table 7.3: Values for EMPHASIS= Option

number	string	Description
0	BALANCE	Performs a balanced search
1	OPTIMAL	Emphasizes optimality over feasibility
2	FEASIBLE	Emphasizes feasibility over optimality

The default value is BALANCE.

FEASTOL=number

specifies the tolerance used to check the feasibility of a solution. This tolerance applies both to the maximum violation of bounds on variables and to the difference between the right-hand sides and left-hand sides of constraints. The value of number can be any value between (and including) 1E–4 and 1E–9. The default value is 1E–6.

If the MILP solver fails to find a feasible solution within this tolerance but does find a solution with a slightly larger violation, then the solver ends with a solution status of OPTIMAL_COND (see the section Macro Variable _OROPTMODEL_ ).

INTTOL=number

specifies the amount by which an integer variable value can differ from an integer and still be considered integer feasible. The value of number can be any number between 0.0 and 1.0; the default value is 1E–5. The MILP solver attempts to find an optimal solution with integer infeasibility less than number. If you assign a value smaller than 1E–10 to number and the best solution found by the solver has integer infeasibility between number and 1E–10, then the solver terminates with a solution status of OPTIMAL_COND (see the section Macro Variable _OROPTMODEL_ ).

LOGFREQ=number PRINTFREQ=number

specifies how often information is printed in the node log. The value of number can be any nonnegative number up to the largest four-byte signed integer, which is 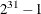$2^{31} - 1$ . The default value of number is 100. If number is set to 0, then the node log is disabled. If number is positive, then an entry is made in the node log at the first node, at the last node, and at intervals dictated by the value of number. An entry is also made each time a better integer solution is found.

LOGLEVEL=number | string PRINTLEVEL2=number | string

controls the amount of information displayed in the SAS log by the MILP solver, from a short description of presolve information and summary to details at each node. Table 7.4 describes the valid values for this option.

Table 7.4: Values for LOGLEVEL= Option

number	string	Description
0	NONE	Turns off all solver-related messages to SAS log
1	BASIC	Displays a solver summary after stopping
2	MODERATE	Prints a solver summary and a node log by using the interval dictated by the LOGFREQ= option
3	AGGRESSIVE	Prints a detailed solver summary and a node log by using the interval dictated by the LOGFREQ= option

The default value is MODERATE.

MAXNODES=number

specifies the maximum number of branch-and-bound nodes to be processed. The value of number can be any nonnegative integer up to the largest four-byte signed integer, which is 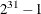$2^{31} - 1$ . The default value of number is $2^{31} - 1$ .

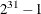MAXSOLS=number

specifies a stopping criterion. If number solutions have been found, then the solver stops. The value of number can be any positive integer up to the largest four-byte signed integer, which is 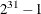$2^{31} - 1$ . The default value of number is $2^{31} - 1$ .

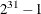MAXTIME=t

specifies an upper limit of t units of time for the optimization process, including problem generation time and solution time. The value of the TIMETYPE= option determines the type of units used. If you do not specify the MAXTIME= option, the solver does not stop based on the amount of time elapsed. The value of t can be any positive number; the default value is the positive number that has the largest absolute value that can be represented in your operating environment.

OPTTOL=number

specifies the tolerance used to determine the optimality of nodes in the branch-and-bound tree. The value of number can be any value between (and including) 1E–4 and 1E–9. The default is 1E–6.

PROBE=number | string

specifies a probing string or its corresponding value number, as listed in the following table:

Table 7.5: Values for PROBE= Option

number	string	Description
–1	AUTOMATIC	Uses the probing strategy determined by the MILP solver
0	NONE	Disables probing
1	MODERATE	Uses probing moderately
2	AGGRESSIVE	Uses probing aggressively

The default value is AUTOMATIC.

RELOBJGAP=number

specifies a stopping criterion based on the best integer objective (BestInteger) and the objective of the best remaining node (BestBound). The relative objective gap is equal to

$\mid \mbox{BestInteger} - \mbox{BestBound}\mid / \left(\mbox{1E$-$10}~ + \mid \mbox{BestBound}\mid \right)$

When this value becomes smaller than the specified gap size number, the solver stops. The value of number can be any nonnegative number; the default value is 1E–4.

SCALE=option

indicates whether to scale the problem matrix. SCALE= can take either of the values AUTOMATIC (–1) and NONE (0). SCALE=AUTOMATIC scales the matrix as determined by the MILP solver; SCALE=NONE disables scaling. The default value is AUTOMATIC.

TARGET=number

specifies a stopping criterion for minimization (maximization) problems. If the best integer objective is better than or equal to number, the solver stops. The value of number can be any number; the default value is the negative (positive) number that has the largest absolute value representable in your operating environment.

TIMETYPE=string 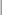$\mid$ number

specifies the units of time used by the MAXTIME= option and reported by the PRESOLVE_TIME and SOLUTION_TIME terms in the _OROPTMODEL_ macro variable. Table 7.6 describes the valid values of the TIMETYPE= option.

Table 7.6: Values for TIMETYPE= Option

number	string	Description
0	CPU	Specifies units of CPU time
1	REAL	Specifies units of real time

The Optimization Statistics table, an output of PROC OPTMODEL if option PRINTLEVEL=2 is specified in the PROC OPTMODEL statement, also includes the same time units for “Presolver Time” and “Solver Time.” The other times (such as “Problem Generation Time”) in the Optimization Statistics table are always CPU times.

The default value of the TIMETYPE= option depends on the values of the NTHREADS= and NODES= options in the PERFORMANCE statement of the OPTMODEL procedure. See the section PERFORMANCE Statement in Chapter 4: Shared Concepts and Topics. for more information about the NTHREADS= and NODES= options.

If you specify a value greater than 1 for either the NTHREADS= or the NODES= option, the default value of the TIMETYPE= option is REAL. If you specify a value of 1 for both the NTHREADS= and NODES= options, the default value of the TIMETYPE= option is CPU.

Heuristics Option

HEURISTICS=number | string

controls the level of primal heuristics applied by the MILP solver. This level determines how frequently primal heuristics are applied during the branch-and-bound tree search. It also affects the maximum number of iterations allowed in iterative heuristics. Some computationally expensive heuristics might be disabled by the solver at less aggressive levels. The values of string and the corresponding values of number are listed in Table 7.7.

Table 7.7: Values for HEURISTICS= Option

number	string	Description
–1	AUTOMATIC	Applies default level of heuristics, similar to MODERATE
0	NONE	Disables all primal heuristics
1	BASIC	Applies basic primal heuristics at low frequency
2	MODERATE	Applies most primal heuristics at moderate frequency
3	AGGRESSIVE	Applies all primal heuristics at high frequency

Setting HEURISTICS=NONE does not disable the heuristics that repair an infeasible input solution that is specified by using the PRIMALIN option.

The default value is AUTOMATIC. For details about primal heuristics, see the section Primal Heuristics.

Search Options

CONFLICTSEARCH=number | string

specifies the level of conflict search performed by the MILP solver. Conflict finds clauses resulting from infeasible subproblems that arise in the search tree. The values of string and the corresponding values of number are listed in Table 7.8.

Table 7.8: Values for CONFLICTSEARCH= Option

number	string	Description
–1	AUTOMATIC	Performs conflict search based on a strategy determined by the MILP solver
0	NONE	Disables conflict search
1	MODERATE	Performs a moderate conflict search
2	AGGRESSIVE	Performs an aggressive conflict search

The default value is AUTOMATIC.

NODESEL=number | string

specifies the node selection strategy string or its corresponding value number as listed in Table 7.9.

Table 7.9: Values for NODESEL= Option

number	string	Description
–1	AUTOMATIC	Uses automatic node selection
0	BESTBOUND	Chooses the node with the best relaxed objective (best-bound-first strategy)
1	BESTESTIMATE	Chooses the node with the best estimate of the integer objective value (best-estimate-first strategy)
2	DEPTH	Chooses the most recently created node (depth-first strategy)

The default value is AUTOMATIC. For details about node selection, see the section Node Selection.

PRIORITY=0 $\mid$ 1

indicates whether to use specified branching priorities for integer variables. PRIORITY=0 ignores variable priorities; PRIORITY=1 uses priorities when they exist. The default value is 1. See the section Branching Priorities for details.

STRONGITER=number | AUTOMATIC

specifies the number of simplex iterations performed for each variable in the candidate list when the strong branching variable selection strategy is used. The value of number can be any positive integer up to the largest four-byte signed integer, which is 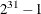$2^{31} - 1$ . If you specify the keyword AUTOMATIC or the value –1, the MILP solver uses the default value; this value is calculated automatically.

STRONGLEN=number | AUTOMATIC

specifies the number of candidates used when the strong branching variable selection strategy is performed. The value of number can be any positive integer up to the largest four-byte signed integer, which is 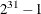$2^{31} - 1$ . If you specify the keyword AUTOMATIC or the value –1, the MILP solver uses the default value; this value is calculated automatically.

VARSEL=number | string

specifies the rule for selecting the branching variable. The values of string and the corresponding values of number are listed in Table 7.10.

Table 7.10: Values for VARSEL= Option

number	string	Description
–1	AUTOMATIC	Uses automatic branching variable selection
0	MAXINFEAS	Chooses the variable with maximum infeasibility
1	MININFEAS	Chooses the variable with minimum infeasibility
2	PSEUDO	Chooses a branching variable based on pseudocost
3	STRONG	Uses strong branching variable selection strategy

The default value is AUTOMATIC. For details about variable selection, see the section Variable Selection.

Cut Options

Table 7.11 describes the string and number values for the cut options in the OPTMODEL procedure.

Table 7.11: Values for Individual Cut Options

number	string	Description
–1	AUTOMATIC	Generates cutting planes based on a strategy determined by the MILP solver
0	NONE	Disables generation of cutting planes
1	MODERATE	Uses a moderate cut strategy
2	AGGRESSIVE	Uses an aggressive cut strategy

You can specify the CUTSTRATEGY= option to set the overall aggressiveness of the cut generation in the MILP solver. Alternatively, you can use the ALLCUTS= option to set all cut types to the same level. You can override the ALLCUTS= value by using the options that correspond to particular cut types. For example, if you want the MILP solver to generate only Gomory cuts, specify ALLCUTS=NONE and CUTGOMORY=AUTOMATIC. If you want to generate all cuts aggressively but generate no lift-and-project cuts, set ALLCUTS=AGGRESSIVE and CUTLAP=NONE.

ALLCUTS=number | string: provides a shorthand way of setting all the cuts-related options in one setting. In other words, ALLCUTS=number is equivalent to setting each of the individual cuts parameters to the same value number. Thus, ALLCUTS=–1 has the effect of setting CUTCLIQUE=–1, CUTFLOWCOVER=–1, CUTFLOWPATH=–1, …, CUTMIR=–1, and CUTZEROHALF=–1. Table 7.11 lists the values that can be assigned to option and number. In addition, you can override levels for individual cuts with the CUTCLIQUE=, CUTFLOWCOVER=, CUTFLOWPATH=, CUTGOMORY=, CUTGUB=, CUTIMPLIED=, CUTKNAPSACK=, CUTLAP=, CUTMILIFTED=, CUTMIR=, and CUTZEROHALF= options. If the ALLCUTS= option is not specified, then all the cuts-related options are either at their individually specified values (if the corresponding option is specified) or at their default values (if that option is not specified).
CUTCLIQUE=number | string: specifies the level of clique cuts that are generated by the MILP solver. Table 7.11 lists the values that can be assigned to option and number. The CUTCLIQUE= option overrides the ALLCUTS= option. The default value is AUTOMATIC.
CUTFLOWCOVER=number | string: specifies the level of flow cover cuts that are generated by the MILP solver. Table 7.11 lists the values that can be assigned to option and number. The CUTFLOWCOVER= option overrides the ALLCUTS= option. The default value is AUTOMATIC.
CUTFLOWPATH=number | string: specifies the level of flow path cuts that are generated by the MILP solver. Table 7.11 lists the values that can be assigned to option and number. The CUTFLOWPATH= option overrides the ALLCUTS= option. The default value is AUTOMATIC.
CUTGOMORY=number | string: specifies the level of Gomory cuts that are generated by the MILP solver. Table 7.11 lists the values that can be assigned to option and number. The CUTGOMORY= option overrides the ALLCUTS= option. The default value is AUTOMATIC.
CUTGUB=number | string: specifies the level of generalized upper bound (GUB) cover cuts that are generated by the MILP solver. Table 7.11 lists the values that can be assigned to option and number. The CUTGUB= option overrides the ALLCUTS= option. The default value is AUTOMATIC.
CUTIMPLIED=number | string: specifies the level of implied bound cuts that are generated by the MILP solver. Table 7.11 lists the values that can be assigned to option and number. The CUTIMPLIED= option overrides the ALLCUTS= option. The default value is AUTOMATIC.
CUTKNAPSACK=number | string: specifies the level of knapsack cover cuts that are generated by the MILP solver. Table 7.11 lists the values that can be assigned to option and number. The CUTKNAPSACK= option overrides the ALLCUTS= option. The default value is AUTOMATIC.
CUTLAP=number | string: specifies the level of lift-and-project (LAP) cuts that are generated by the MILP solver. Table 7.11 lists the values that can be assigned to option and number. The CUTLAP= option overrides the ALLCUTS= option. The default value is NONE.
CUTMILIFTED=number | string: specifies the level of mixed lifted 0-1 cuts that are generated by the MILP solver. Table 7.11 lists the values that can be assigned to option and number. The CUTMILIFTED= option overrides the ALLCUTS= option. The default value is AUTOMATIC.
CUTMIR=number | string: specifies the level of mixed integer rounding (MIR) cuts that are generated by the MILP solver. Table 7.11 lists the values that can be assigned to option and number. The CUTMIR= option overrides the ALLCUTS= option. The default value is AUTOMATIC.
CUTSFACTOR=number: specifies a row multiplier factor for cuts. The number of cuts that are added is limited to number times the original number of rows. The value of number can be any nonnegative number less than or equal to 100; the default value is automatically calculated by the MILP solver.
CUTSTRATEGY=number | string CUTS=number | string: specifies the overall aggressiveness of the cut generation in the solver. Setting a nondefault value adjusts a number of cut parameters such that the cut generation is basic, moderate, or aggressive compared to the default value.
CUTZEROHALF=number | string: specifies the level of zero-half cuts that are generated by the MILP solver. Table 7.11 lists the values that can be assigned to option and number.The CUTZEROHALF= option overrides the ALLCUTS= option. The default value is AUTOMATIC.

Decomposition Algorithm Options

The following options are available for the decomposition algorithm in the MILP solver. For information about the decomposition algorithm, see Chapter 13: The Decomposition Algorithm.

DECOMP=(options): enables the decomposition algorithm and specifies overall control options for the algorithm. For more information about this option, see Chapter 13: The Decomposition Algorithm.
DECOMP_MASTER=(options): specifies options for the master problem. For more information about this option, see Chapter 13: The Decomposition Algorithm.
DECOMP_MASTER_IP=(options): specifies options for the (restricted) master problem solved as a MILP with the current set of columns in an effort to obtain an integer feasible solution. For more information about this option, see Chapter 13: The Decomposition Algorithm.
DECOMP_SUBPROB=(options): specifies option for the subproblem. For more information about this option, see Chapter 13: The Decomposition Algorithm.

The Mixed Integer Linear Programming Solver