| A Transportation Problem |
You can easily translate the symbolic formulation of a problem into the OPTMODEL procedure. Consider the transportation problem, which is mathematically modeled as the following linear programming problem:
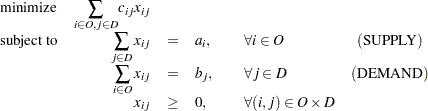 |
where 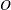 is the set of origins,
is the set of origins,  is the set of destinations,
is the set of destinations, 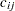 is the cost to transport one unit from
is the cost to transport one unit from 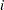 to
to 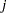 ,
, 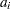 is the supply of origin
is the supply of origin 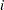 ,
, 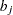 is the demand of destination
is the demand of destination 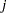 , and
, and 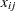 is the decision variable for the amount of shipment from
is the decision variable for the amount of shipment from 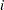 to
to 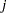 .
.
Here is a very simple example. The cities in the set 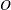 of origins are Detroit and Pittsburgh. The cities in the set
of origins are Detroit and Pittsburgh. The cities in the set  of destinations are Boston and New York. The cost matrix, supply, and demand are shown in Table 4.2.
of destinations are Boston and New York. The cost matrix, supply, and demand are shown in Table 4.2.
Boston |
New York |
Supply |
|
Detroit |
30 |
20 |
200 |
Pittsburgh |
40 |
10 |
100 |
Demand |
150 |
150 |
The problem is compactly and clearly formulated and solved by using the OPTMODEL procedure with the following statements:
proc optmodel;
/* specify parameters */
set O={'Detroit','Pittsburgh'};
set D={'Boston','New York'};
number c{O,D}=[30 20
40 10];
number a{O}=[200 100];
number b{D}=[150 150];
/* model description */
var x{O,D} >= 0;
min total_cost = sum{i in O, j in D}c[i,j]*x[i,j];
constraint supply{i in O}: sum{j in D}x[i,j]=a[i];
constraint demand{j in D}: sum{i in O}x[i,j]=b[j];
/* solve and output */
solve;
print x;
The output is shown in Figure 4.4.
| Problem Summary | |
|---|---|
| Objective Sense | Minimization |
| Objective Function | total_cost |
| Objective Type | Linear |
| Number of Variables | 4 |
| Bounded Above | 0 |
| Bounded Below | 4 |
| Bounded Below and Above | 0 |
| Free | 0 |
| Fixed | 0 |
| Number of Constraints | 4 |
| Linear LE (<=) | 0 |
| Linear EQ (=) | 4 |
| Linear GE (>=) | 0 |
| Linear Range | 0 |
| Constraint Coefficients | 8 |
| Solution Summary | |
|---|---|
| Solver | Dual Simplex |
| Objective Function | total_cost |
| Solution Status | Optimal |
| Objective Value | 6500 |
| Iterations | 0 |
| Primal Infeasibility | 0 |
| Dual Infeasibility | 0 |
| Bound Infeasibility | 0 |
| x | ||
|---|---|---|
| Boston | New York | |
| Detroit | 150 | 50 |
| Pittsburgh | 0 | 100 |