The OPTMILP Procedure
Example 11.1 Simple Integer Linear Program
This example illustrates a model in an MPS-format SAS data set. This data set is passed to PROC OPTMILP, and a solution is found.
Consider a scenario where you have a container with a set of limiting attributes (volume  and weight
and weight 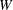 ) and a set
) and a set 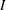 of items that you want to pack. Each item type
of items that you want to pack. Each item type  has a certain value
has a certain value  , a volume
, a volume 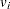 , and a weight
, and a weight 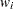 . You must choose at most four items of each type so that the total value is maximized and all the chosen items fit into the container. Let
. You must choose at most four items of each type so that the total value is maximized and all the chosen items fit into the container. Let 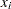 be the number of items of type
be the number of items of type  to be included in the container. This model can be formulated as the following integer linear program:
to be included in the container. This model can be formulated as the following integer linear program:
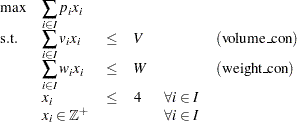 |
Constraint (volume_con) enforces the volume capacity limit, while constraint (weight_con) enforces the weight capacity limit. An instance of this problem can be saved in an MPS-format SAS data set by using the following code:
data ex1data;
input field1 $ field2 $ field3 $ field4 field5 $ field6;
datalines;
NAME . ex1data . . .
ROWS . . . . .
MAX z . . . .
L volume_con . . . .
L weight_con . . . .
COLUMNS . . . . .
. .MRK0 'MARKER' . 'INTORG' .
. x[1] z 1 volume_con 10
. x[1] weight_con 12 . .
. x[2] z 2 volume_con 300
. x[2] weight_con 15 . .
. x[3] z 3 volume_con 250
. x[3] weight_con 72 . .
. x[4] z 4 volume_con 610
. x[4] weight_con 100 . .
. x[5] z 5 volume_con 500
. x[5] weight_con 223 . .
. x[6] z 6 volume_con 120
. x[6] weight_con 16 . .
. x[7] z 7 volume_con 45
. x[7] weight_con 73 . .
. x[8] z 8 volume_con 100
. x[8] weight_con 12 . .
. x[9] z 9 volume_con 200
. x[9] weight_con 200 . .
. x[10] z 10 volume_con 61
. x[10] weight_con 110 . .
. .MRK1 'MARKER' . 'INTEND' .
RHS . . . . .
. .RHS. volume_con 1000 . .
. .RHS. weight_con 500 . .
BOUNDS . . . . .
UP .BOUNDS. x[1] 4 . .
UP .BOUNDS. x[2] 4 . .
UP .BOUNDS. x[3] 4 . .
UP .BOUNDS. x[4] 4 . .
UP .BOUNDS. x[5] 4 . .
UP .BOUNDS. x[6] 4 . .
UP .BOUNDS. x[7] 4 . .
UP .BOUNDS. x[8] 4 . .
UP .BOUNDS. x[9] 4 . .
UP .BOUNDS. x[10] 4 . .
ENDATA . . . . .
;
In the COLUMNS section of this data set, the name of the objective is z, and the objective coefficients  appear in field4. The coefficients
appear in field4. The coefficients 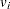 of (volume_con) appear in field6. The coefficients
of (volume_con) appear in field6. The coefficients 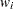 of (weight_con) appear in field4. In the RHS section, the bounds
of (weight_con) appear in field4. In the RHS section, the bounds  and
and 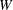 appear in field4.
appear in field4.
This problem can be solved by using the following statements to call the OPTMILP procedure:
proc optmodel;
num nItems = 10;
num volume_capacity = 1000;
num weight_capacity = 500;
set<num> Items = {1..nItems};
num value{Items} = [1,2,3,4,5,6,7,8,9,10];
num volume{Items} = [10, 300, 250, 610, 500, 120, 45, 100, 200, 61 ];
num weight{Items} = [12, 15, 72, 100, 223, 16, 73, 12, 200, 110];
var x{Items} integer >= 0 <= 4;
max z = sum{i in Items} value[i] * x[i];
con volume_con: sum{i in Items} volume[i] * x[i] <= volume_capacity;
con weight_con: sum{i in Items} weight[i] * x[i] <= weight_capacity;
save mps ex1data;
quit;
run;
proc optmilp data=ex1data primalout=ex1soln;
run;
The progress of the solver is shown in Output 11.1.1.
| NOTE: The problem ex1data has 10 variables (0 binary, 10 integer, 0 free, 0 |
| fixed). |
| NOTE: The problem has 2 constraints (2 LE, 0 EQ, 0 GE, 0 range). |
| NOTE: The problem has 20 constraint coefficients. |
| NOTE: The OPTMILP presolver value AUTOMATIC is applied. |
| NOTE: The OPTMILP presolver removed 0 variables and 0 constraints. |
| NOTE: The OPTMILP presolver removed 0 constraint coefficients. |
| NOTE: The OPTMILP presolver modified 0 constraint coefficients. |
| NOTE: The presolved problem has 10 variables, 2 constraints, and 20 constraint |
| coefficients. |
| NOTE: The MIXED INTEGER LINEAR solver is called. |
| Node Active Sols BestInteger BestBound Gap Time |
| 0 1 3 85.0000000 178.0000000 52.25% 0 |
| 0 1 3 85.0000000 88.0955497 3.51% 0 |
| 0 1 3 85.0000000 87.8923914 3.29% 0 |
| 0 1 4 86.0000000 87.8372425 2.09% 0 |
| 0 1 4 86.0000000 87.8342067 2.09% 0 |
| 0 1 4 86.0000000 87.8319845 2.09% 0 |
| 0 1 4 86.0000000 87.7893284 2.04% 0 |
| 0 1 4 86.0000000 87.7891271 2.04% 0 |
| NOTE: OPTMILP added 3 cuts with 30 cut coefficients at the root. |
| 5 0 5 87.0000000 . 0.00% 0 |
| NOTE: Optimal. |
| NOTE: Objective = 87. |
| NOTE: The data set WORK.EX1SOLN has 10 observations and 8 variables. |
The data set ex1soln is shown in Output 11.1.2.
| Example 1 Solution Data |
| Objective Function ID |
RHS ID | Variable Name | Variable Type |
Objective Coefficient |
Lower Bound |
Upper Bound |
Variable Value |
|---|---|---|---|---|---|---|---|
| z | .RHS. | x[1] | I | 1 | 0 | 4 | 0 |
| z | .RHS. | x[2] | I | 2 | 0 | 4 | 0 |
| z | .RHS. | x[3] | I | 3 | 0 | 4 | 0 |
| z | .RHS. | x[4] | I | 4 | 0 | 4 | 0 |
| z | .RHS. | x[5] | I | 5 | 0 | 4 | 0 |
| z | .RHS. | x[6] | I | 6 | 0 | 4 | 3 |
| z | .RHS. | x[7] | I | 7 | 0 | 4 | 1 |
| z | .RHS. | x[8] | I | 8 | 0 | 4 | 4 |
| z | .RHS. | x[9] | I | 9 | 0 | 4 | 0 |
| z | .RHS. | x[10] | I | 10 | 0 | 4 | 3 |
The optimal solution is 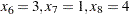 , and
, and  , with a total value of
, with a total value of 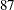 . From this solution, you can compute the total volume used, which is 988 (
. From this solution, you can compute the total volume used, which is 988 (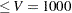 ); the total weight used is 499 (
); the total weight used is 499 (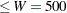 ). The problem summary and solution summary are shown in Output 11.1.3.
). The problem summary and solution summary are shown in Output 11.1.3.
proc optmodel;
num nItems = 10;
num volume_capacity = 1000;
num weight_capacity = 500;
set<num> Items = {1..nItems};
num value{Items} = [1,2,3,4,5,6,7,8,9,10];
num volume{Items} = [10, 300, 250, 610, 500, 120, 45, 100, 200, 61 ];
num weight{Items} = [12, 15, 72, 100, 223, 16, 73, 12, 200, 110];
var x{Items} integer >= 0 <= 4;
max z = sum{i in Items} value[i] * x[i];
con volume_con: sum{i in Items} volume[i] * x[i] <= volume_capacity;
con weight_con: sum{i in Items} weight[i] * x[i] <= weight_capacity;
save mps ex1data;
quit;
run;
proc optmilp data=ex1data primalout=ex1soln;
title ' ';
run;
| Problem Summary | |
|---|---|
| Problem Name | ex1data |
| Objective Sense | Maximization |
| Objective Function | z |
| RHS | .RHS. |
| Number of Variables | 10 |
| Bounded Above | 0 |
| Bounded Below | 0 |
| Bounded Above and Below | 10 |
| Free | 0 |
| Fixed | 0 |
| Binary | 0 |
| Integer | 10 |
| Number of Constraints | 2 |
| LE (<=) | 2 |
| EQ (=) | 0 |
| GE (>=) | 0 |
| Range | 0 |
| Constraint Coefficients | 20 |
| Solution Summary | |
|---|---|
| Objective Function | z |
| Solution Status | Optimal |
| Objective Value | 87 |
| Relative Gap | 0 |
| Absolute Gap | 0 |
| Primal Infeasibility | 0 |
| Bound Infeasibility | 0 |
| Integer Infeasibility | 0 |
| Best Bound | . |
| Nodes | 6 |
| Iterations | 30 |
| Presolve Time | 0.00 |
| Solution Time | 0.02 |
