specifies the maximum number of iterations. The value can be any integer between one and the largest four-byte signed integer, which is . If you do not specify this option, the procedure does not stop based on the number of iterations performed.

specifies an upper limit of seconds of real time for the optimization process. If you do not specify this option, the procedure does not stop based on the amount of time elapsed.

specifies one of the following presolve options:

You can also specify the option by integers from 1 to 3. The integer value for each option is indicated in parentheses. The default option is AUTOMATIC.

specifies that the printing of the solution progress to the iteration log is to occur after every iterations. The print frequency, , is an integer between zero and the largest four-byte signed integer, which is .

The value disables the printing of the progress of the solution. The default value of this option is 1.

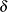
specifies the desired relative duality gap, 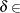[1E–9, 1E–4]. This is the relative difference between the primal and dual objective function values and is the primary solution quality parameter. The default value is 1E–6. See the section Interior Point Algorithm: Overview for details.

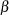
specifies the maximum allowed relative dual constraints violation, 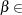[1E–9, 1E–4]. The default value is 1E–6. See the section Interior Point Algorithm: Overview for details.

specifies the maximum allowed relative bound and primal constraints violation, [1E–9, 1E–4]. The default value is 1E–6. See the section Interior Point Algorithm: Overview for details.