The QP solver implements an infeasible primal-dual predictor-corrector interior point algorithm. To illustrate the algorithm and the concepts of duality and dual infeasibility, consider the following QP formulation (the primal):

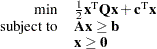The corresponding dual is as follows:

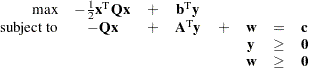where 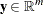refers to the vector of dual variables and 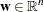refers to the vector of dual slack variables.

The dual makes an important contribution to the certificate of optimality for the primal. The primal and dual constraints combined with complementarity conditions define the first-order optimality conditions, also known as KKT (Karush-Kuhn-Tucker) conditions, which can be stated as follows:

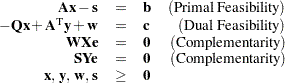where of appropriate dimension and 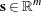is the vector of primal slack variables.

Note:Slack variables (the vector) are automatically introduced by the solver when necessary; it is therefore recommended that you not introduce any slack variables explicitly. This enables the solver to handle slack variables much more efficiently.

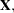
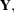
The letters and denote matrices with corresponding 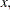and on the main diagonal and zero elsewhere, as in the following example:

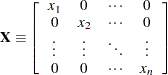If 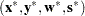is a solution of the previously defined system of equations representing the KKT conditions, then 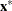is also an optimal solution to the original QP model.

At each iteration the interior point algorithm solves a large, sparse system of linear equations as follows:

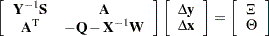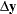where and denote the vector of search directions in the primal and dual spaces, respectively; 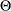and 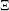constitute the vector of the right-hand sides.

The preceding system is known as the reduced KKT system. The QP solver uses a preconditioned quasi-minimum residual algorithm to solve this system of equations efficiently.

An important feature of the interior point algorithm is that it takes full advantage of the sparsity in the constraint and quadratic matrices, thereby enabling it to efficiently solve large-scale quadratic programs.

The interior point algorithm works simultaneously in the primal and dual spaces. It attains optimality when both primal and dual feasibility are achieved and when complementarity conditions hold. Therefore it is of interest to observe the following four measures:

• Relative primal infeasibility measure :

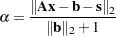
• Relative dual infeasibility measure :

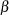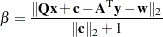
• Relative duality gap :

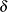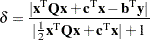
• Absolute complementarity :

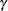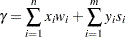
where 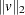is the Euclidean norm of the vector . These measures are displayed in the iteration log.