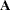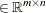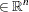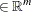| The Quadratic Programming Solver |
Overview: QP Solver
The OPTMODEL procedure provides a framework for specifying and solving quadratic programs.
Mathematically, a quadratic programming (QP) problem can be stated as follows:
 |
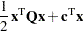 |
|||
 |
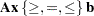 |
|||
 |
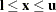 |
where
|
|
is the quadratic (also known as Hessian) matrix |
|
|
is the constraints matrix |
|
|
is the vector of decision variables |
|
|
is the vector of linear objective function coefficients |
|
|
is the vector of constraints right-hand sides (RHS) |
|
|
is the vector of lower bounds on the decision variables |
|
|
is the vector of upper bounds on the decision variables |
The quadratic matrix  is assumed to be symmetric; i.e.,
is assumed to be symmetric; i.e.,
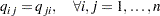 |
Indeed, it is easy to show that even if  , then the simple modification
, then the simple modification
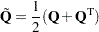 |
produces an equivalent formulation 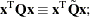 hence symmetry is assumed. When specifying a quadratic matrix it suffices to list only lower triangular coefficients.
hence symmetry is assumed. When specifying a quadratic matrix it suffices to list only lower triangular coefficients.
In addition to being symmetric,  is also required to be positive semidefinite:
is also required to be positive semidefinite:
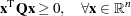 |
for minimization type of models; it is required to be negative semidefinite for maximization type of models. Convexity can come as a result of a matrix-matrix multiplication
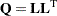 |
or as a consequence of physical laws, etc. See Figure 14.1 for examples of convex, concave, and nonconvex objective functions.
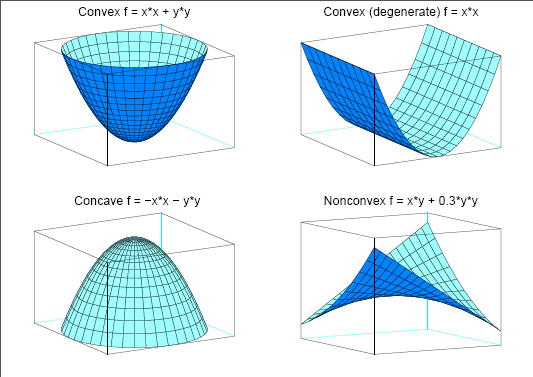
The order of constraints is insignificant. Some or all components of  or
or  (lower/upper bounds) can be omitted.
(lower/upper bounds) can be omitted.
Note: This procedure is experimental.
Copyright © SAS Institute, Inc. All Rights Reserved.