PROC OPTQP: Portfolio Selection with Transactions :: SAS/OR(R) 9.22 User's Guide: Mathematical Programming

The OPTQP Procedure

Example 19.3 Portfolio Selection with Transactions

Consider a portfolio selection problem with a slight modification. You are now required to take into account the current position and transaction costs associated with buying and selling assets. The objective is to find the minimum variance portfolio. In order to understand the scenario better, consider the following data.

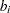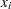You are given three assets. The current holding of the three assets is denoted by the vector $\text{[math]}$ = [200, 300, 500], the amount of asset bought and sold is denoted by $\text{[math]}$ and $\text{[math]}$ , respectively, and the net investment in each asset is denoted by $\text{[math]}$ and is defined by the following relation:

$\text{[math]}$

Let us say that you pay a transaction fee of 0.01 every time you buy or sell. Let the covariance matrix $\text{[math]}$ be defined as

$\text{[math]}$

Assume that you hope to obtain at least 12% growth. Let $\text{[math]}$ = [1.109048, 1.169048, 1.074286] be the vector of expected return on the three assets, and let $\text{[math]}$ =1000 be the available funds. Mathematically, this problem can be written in the following manner:

$\text{[math]}$

The QPS-format input data set is as follows:

data potrdata;
   input field1 $ field2 $ field3$ field4 field5 $ field6 @;
datalines;
NAME  .        POTRAN    .              .          .  
ROWS  .        .         .              .          .
N    OBJ.FUNC  .         .              .          .
G    RETURN    .         .              .          .
E    BUDGET    .         .              .          .
E    BALANC1   .         .              .          .
E    BALANC2   .         .              .          .
E    BALANC3   .         .              .          .
COLUMNS .      .         .              .          .
.    X1        RETURN    1.109048       BUDGET     1.0
.    X1        BALANC1   1.0            .          .
.    X2        RETURN    1.169048       BUDGET     1.0
.    X2        BALANC2   1.0            .          .
.    X3        RETURN    1.074286       BUDGET     1.0
.    X3        BALANC3   1.0            .          .
.    B1        BUDGET    .01            BALANC1   -1.0
.    B2        BUDGET    .01            BALANC2   -1.0
.    B3        BUDGET    .01            BALANC3   -1.0
.    S1        BUDGET    .01            BALANC1    1.0
.    S2        BUDGET    .01            BALANC2    1.0
.    S3        BUDGET    .01            BALANC3    1.0
RHS  .         .         .              .          .
.    RHS       RETURN    1120           .          .
.    RHS       BUDGET    1000           .          .
.    RHS       BALANC1   200            .          .
.    RHS       BALANC2   300            .          .
.    RHS       BALANC3   500            .          .
RANGES .       .         .              .          .
BOUNDS .       .         .              .          .
QUADOBJ .      .         .              .          .
.    X1        X1        0.054978       .          .
.    X1        X2        -.01748        .          .
.    X1        X3        -.0003         .          .
.    X2        X2        0.218898       .          .
.    X2        X3        -.00024        .          .
.    X3        X3        0.001532       .          .
ENDATA .       .         .              .          .
;

Use the following SAS code to solve the problem:

proc optqp data=potrdata 
  primalout = potrpout 
  printlevel = 0
  dualout   = potrdout;
run;

The optimal solution is displayed in Output 19.3.1.

Output 19.3.1 Portfolio Selection with Transactions

The OPTQP Procedure

Primal Solution

Obs	Objective Function ID	RHS ID	Variable Name	Variable Type	Upper Bound	Variable Value	Variable Status
1	OBJ.FUNC	RHS	X1	N	1.7977E308	397.584	O
2	OBJ.FUNC	RHS	X2	N	1.7977E308	406.115	O
3	OBJ.FUNC	RHS	X3	N	1.7977E308	190.165	O
4	OBJ.FUNC	RHS	B1	N	1.7977E308	197.584	O
5	OBJ.FUNC	RHS	B2	N	1.7977E308	106.115	O
6	OBJ.FUNC	RHS	B3	N	1.7977E308	0.000	O
7	OBJ.FUNC	RHS	S1	N	1.7977E308	0.000	O
8	OBJ.FUNC	RHS	S2	N	1.7977E308	0.000	O
9	OBJ.FUNC	RHS	S3	N	1.7977E308	309.835	O

Top of Page