| The OPTQP Procedure |
Example 19.1 Linear Least Squares Problem
The linear least squares problem arises in the context of determining a solution to an over-determined set of linear equations. In practice, these could arise in data fitting and estimation problems. An 1 system of linear equations can be defined as
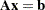 |
where  ,
, 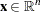 ,
, 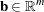 , and
, and 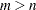 . Since this system usually does not have a solution, we need to be satisfied with some sort of approximate solution. The most widely used approximation is the least squares solution, which minimizes
. Since this system usually does not have a solution, we need to be satisfied with some sort of approximate solution. The most widely used approximation is the least squares solution, which minimizes 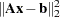 .
.
This problem is called a least squares problem for the following reason. Let 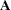 ,
,  , and
, and 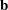 be defined as previously. Let
be defined as previously. Let 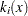 be the
be the  th component of the vector
th component of the vector  :
:
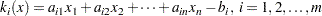 |
By definition of the Euclidean norm, the objective function can be expressed as follows:
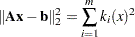 |
Therefore, the function we minimize is the sum of squares of  terms
terms 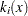 ; hence the term least squares. The following example is an illustration of the linear least squares problem; i.e., each of the terms
; hence the term least squares. The following example is an illustration of the linear least squares problem; i.e., each of the terms 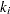 is a linear function of
is a linear function of  .
.
Consider the following least squares problem defined by
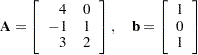 |
This translates to the following set of linear equations:
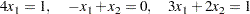 |
The corresponding least squares problem is
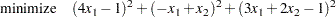 |
The preceding objective function can be expanded to
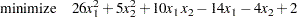 |
In addition, we impose the following constraint so that the equation 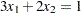 is satisfied within a tolerance of
is satisfied within a tolerance of  :
:
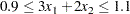 |
You can create the QPS-format input data set by using the following SAS code:
data lsdata; input field1 $ field2 $ field3$ field4 field5 $ field6 @; datalines; NAME . LEASTSQ . . . ROWS . . . . . N OBJ . . . . G EQ3 . . . . COLUMNS . . . . . . X1 OBJ -14 EQ3 3 . X2 OBJ -4 EQ3 2 RHS . . . . . . RHS OBJ -2 EQ3 0.9 RANGES . . . . . . RNG EQ3 0.2 . . BOUNDS . . . . . FR BND1 X1 . . . FR BND1 X2 . . . QUADOBJ . . . . . . X1 X1 52 . . . X1 X2 10 . . . X2 X2 10 . . ENDATA . . . . . ;
The decision variables 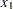 and
and  are free, so they have bound type FR in the BOUNDS section of the QPS-format data set.
are free, so they have bound type FR in the BOUNDS section of the QPS-format data set.
You can use the following SAS code to solve the least squares problem:
proc optqp data=lsdata printlevel = 0 primalout = lspout; run;
The optimal solution is displayed in Output 19.1.1.
The iteration log is shown in Output 19.1.2.
| line |
|---|
| NOTE: The problem LEASTSQ has 2 variables (2 free, 0 fixed). |
| NOTE: The problem has 1 constraints (0 LE, 0 EQ, 0 GE, 1 range). |
| NOTE: The problem has 2 constraint coefficients. |
| NOTE: The objective function has 2 Hessian diagonal elements and 1 Hessian |
| elements above the diagonal. |
| NOTE: The OPTQP presolver value AUTOMATIC is applied. |
| NOTE: The OPTQP presolver removed 0 variables and 0 constraints. |
| NOTE: The OPTQP presolver removed 0 constraint coefficients. |
| NOTE: The QUADRATIC ITERATIVE solver is called. |
| Primal Bound Dual |
| Iter Complement Duality Gap Infeas Infeas Infeas |
| 0 10001805 2.001029 1052.607895 416.588001 0 |
| 1 501893 2.094827 52.630395 20.750266 0 |
| 2 26887 34.114879 2.631520 0.958349 0 |
| 3 2997.321110 600.993085 0.131576 0 0 |
| 4 734.867262 111.975745 0.006579 0 0 |
| 5 26.413788 5.701869 0.000329 0 0 |
| 6 0.877292 0.287945 0.000016608 0 0 |
| 7 0.051222 0.017041 0.000000983 0 0 |
| 8 0.007624 0.001934 0.000000103 0 0 |
| 9 0.001232 0.000171 5.7776383E-9 0 0 |
| 10 0.000047950 0.000008773 2.898554E-10 0 0 |
| 11 0.000001381 0.000000438 1.449273E-11 0 0 |
| NOTE: Optimal. |
| NOTE: Objective = 0.0095238096. |
| NOTE: The data set WORK.LSPOUT has 2 observations and 9 variables. |
Copyright © SAS Institute, Inc. All Rights Reserved.