| The OPTMODEL Procedure |
| The Rosenbrock Problem |
You can use parameters to produce a clear formulation of a problem. Consider the Rosenbrock problem:
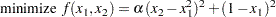 |
where 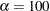 is a parameter (constant),
is a parameter (constant), 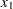 and
and 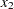 are optimization variables (whose values are to be determined), and
are optimization variables (whose values are to be determined), and 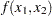 is an objective function.
is an objective function.
Here is a PROC OPTMODEL program that solves the Rosenbrock problem:
proc optmodel;
number alpha = 100; /* declare parameter */
var x {1..2}; /* declare variables */
/* objective function */
min f = alpha*(x[2] - x[1]**2)**2 +
(1 - x[1])**2;
/* now run the solver */
solve;
print x;
quit;
The PROC OPTMODEL output is shown in Figure 8.3.
| Problem Summary | |
|---|---|
| Objective Sense | Minimization |
| Objective Function | f |
| Objective Type | Nonlinear |
| Number of Variables | 2 |
| Bounded Above | 0 |
| Bounded Below | 0 |
| Bounded Below and Above | 0 |
| Free | 2 |
| Fixed | 0 |
| Number of Constraints | 0 |
Copyright © SAS Institute, Inc. All Rights Reserved.