The feasible region of every linear program forms a polyhedron. Every polyhedron in -space can be written as a finite number of half-spaces (equivalently, inequalities). In our notation, this polyhedron is defined by the set 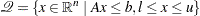. After we add the restriction that some variables must be integral, the set of feasible solutions, 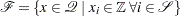, no longer forms a polyhedron.

The convex hull of a set 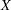is the minimal convex set containing 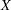. In solving a mixed integer linear program, in order to take advantage of LP-based algorithms we want to find the convex hull, 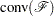, of 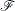. If we can find 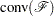and describe it compactly, then we can solve a mixed integer linear program with a linear programming solver. This is generally very difficult, so we must be satisfied with finding an approximation. Typically, the better the approximation, the more efficiently the LP-based branch-and-bound algorithm can perform.

As described in the section The Branch-and-Bound Algorithm, the branch-and-bound algorithm begins by solving the linear programming relaxation over the polyhedron 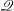. Clearly, 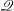contains the convex hull of the feasible region of the original integer program; that is, .

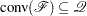Cutting plane techniques are used to tighten the linear relaxation to better approximate 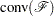. Assume we are given a solution to some intermediate linear relaxation during the branch-and-bound algorithm. A cut, or valid inequality (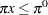), is some half-space with the following characteristics:

• The half-space contains 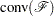; that is, every integer feasible solution is feasible for the cut ().

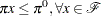• The half-space does not contain the current solution ; that is, is not feasible for the cut ().

Cutting planes were first made popular by Dantzig, Fulkerson, and Johnson (1954) in their work on the traveling salesman problem. The two major classifications of cutting planes are generic cuts and structured cuts. The first class of cuts is based solely on algebraic arguments and can be applied to any relaxation of any integer program. The second class of cuts is specific to certain structures that can be found in some relaxations of the mixed integer linear program. These structures are automatically discovered during the cut initialization phase of PROC OPTMILP. Table 18.10 lists the various types of cutting planes that are built into PROC OPTMILP. Included in each type are algorithms for numerous variations based on different relaxations and lifting techniques. For a survey of cutting plane techniques for mixed integer programming, see Marchand et al. (1999). For a survey of lifting techniques, see Atamturk (2004).

You can set levels for individual cuts by using the CUTCLIQUE=, CUTFLOWCOVER=, CUTFLOWPATH=, CUTGOMORY=, CUTGUB=, CUTIMPLIED=, CUTKNAPSACK=, CUTLAP=, and CUTMIR= options.

The valid levels for these options are given in Table 18.9.

The cut level determines the internal strategy used by PROC OPTMILP for generating the cutting planes. The strategy consists of several factors, including how frequently the cut search is called, the number of cuts allowed, and the aggressiveness of the search algorithms.

Sophisticated cutting planes, such as those included in PROC OPTMILP, can take a great deal of CPU time. Typically the additional tightening of the relaxation helps to speed up the overall process as it provides better bounds for the branch-and-bound tree and helps guide the LP solver toward integer solutions. In rare cases shutting off cutting planes completely might lead to faster overall run times.

The default settings of PROC OPTMILP have been tuned to work well for most instances. However, problem-specific expertise might suggest adjusting one or more of the strategies. These options give you that flexibility.