PROC OPTLP: Finding an Irreducible Infeasible Set :: SAS/OR(R) 9.22 User's Guide: Mathematical Programming

The OPTLP Procedure

Example 17.7 Finding an Irreducible Infeasible Set

This example demonstrates the use of the IIS= option to locate an irreducible infeasible set. Suppose you want to solve a linear program that has the following simple formulation:

$\text{[math]}$

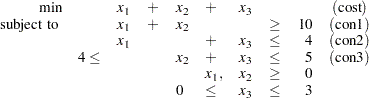The corresponding MPS-format SAS data set is as follows:

 
/* infeasible */
data exiis;
   input field1 $ field2 $ field3 $ field4 field5 $ field6;
datalines;
NAME     .        .        .        .        .
ROWS     .        .        .        .        .
 N       cost     .        .        .        .
 G       con1     .        .        .        .
 L       con2     .        .        .        .
 G       con3     .        .        .        .
COLUMNS  .        .        .        .        .
.        x1       cost     1        con1     1
.        x1       con2     1        .        .
.        x2       cost     1        con1     1
.        x2       con3     1        .        .
.        x3       cost     1        con2     1
.        x3       con3     1        .        .
RHS      .        .        .        .        .
.        rhs      con1     10       con2     4
.        rhs      con3     4        .        .
RANGES   .        .        .        .        .
.        r1       con3     1        .        .
BOUNDS   .        .        .        .        .
UP       b1       x3       3        .        . 
ENDATA   .        .        .        .        .
;

It is easy to verify that the following three constraints (or rows) and one variable (or column) bound form an IIS for this problem.

$\text{[math]}$

You can use the IIS=ON option to detect this IIS by using the following statements:

proc optlp data=exiis
   iis=on
   primalout=iis_vars
   dualout=iis_cons
   printfreq=1;
run;

The OPTLP procedure outputs the detected IIS to the data sets specified by the PRIMALOUT= and DUALOUT= options, then stops. The notes shown in Output 17.7.1 are printed to the log.

Output 17.7.1 The IIS= Option: Log

The OPTLP Procedure

Dual Solution

line


NOTE: The problem has 3 variables (0 free, 0 fixed).
NOTE: The problem has 3 constraints (1 LE, 0 EQ, 1 GE, 1 range).
NOTE: The problem has 6 constraint coefficients.
NOTE: The IIS option is called.
Objective Entering Leaving
Phase Iteration Value Variable Variable
1 1 5.000000 x2 con3 (S)
1 2 1.000000 x1 con2 (S)
NOTE: Processing rows.
1 3 0 con2 (S) con1 (S)
1 4 0 con3 (S) con1 (S)
NOTE: Processing columns.
1 5 0 x3 con1 (S)
NOTE: The IIS option found an IIS set with 3 rows and 1 columns.
NOTE: The data set WORK.IIS_VARS has 3 observations and 10 variables.
NOTE: The data set WORK.IIS_CONS has 3 observations and 10 variables.

The data sets iis_cons and iis_vars are shown in Output 17.7.2.

Output 17.7.2 Identify Rows and Columns in the IIS

Constraints in the IIS

Obs	Objective Function ID	RHS ID	Constraint Name	Constraint Type	Constraint RHS	Constraint Lower Bound	Constraint Upper Bound	Constraint Status
1	cost	rhs	con1	G	10	.	.	I_L
2	cost	rhs	con2	L	4	.	.	I_U
3	cost	rhs	con3	R	.	4	5	I_U

Variables in the IIS

Obs	Objective Function ID	RHS ID	Variable Name	Variable Type	Objective Coefficient	Upper Bound	Variable Status
1	cost	rhs	x1	N	1	1.7977E308
2	cost	rhs	x2	N	1	1.7977E308
3	cost	rhs	x3	D	1	3	I_L

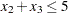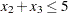The constraint $\text{[math]}$ , which is an element of the IIS, is created by the RANGES section. The original constraint is con3, a " $\text{[math]}$ " constraint with an RHS value of 4. If you choose to remove the constraint $\text{[math]}$ , you can accomplish this by removing con3 from the RANGES section in the MPS-format SAS data set exiis. Since con3 is the only observation in the section, the identifier observation can also be removed. The modified LP problem is specified in the following SAS statements:

 /* droping con3, feasible */
data exiisf;
   input field1 $ field2 $ field3 $ field4 field5 $ field6;
datalines;
NAME     .        .        .        .        .
ROWS     .        .        .        .        .
 N       cost     .        .        .        .
 G       con1     .        .        .        .
 L       con2     .        .        .        .
 G       con3     .        .        .        .
COLUMNS  .        .        .        .        .
.        x1       cost     1        con1     1
.        x1       con2     1        .        .
.        x2       cost     1        con1     1
.        x2       con3     1        .        .
.        x3       cost     1        con2     1
.        x3       con3     1        .        .
RHS      .        .        .        .        .
.        rhs      con1     10       con2     4
.        rhs      con3     4        .        .
BOUNDS   .        .        .        .        .
UP       b1       x3       3        .        . 
ENDATA   .        .        .        .        .
;

Since one element of the IIS has been removed, the modified LP problem should no longer contain the infeasible set. Due to the size of this problem, there should be no additional irreducible infeasible sets. You can confirm this by submitting the following SAS statements:

proc optlp data=exiisf
   pout=po
   iis=on;
run;

The notes shown in Output 17.7.3 are printed to the log.

Output 17.7.3 The IIS= Option: Log

Variables in the IIS

line


NOTE: The problem has 3 variables (0 free, 0 fixed).
NOTE: The problem has 3 constraints (1 LE, 0 EQ, 2 GE, 0 range).
NOTE: The problem has 6 constraint coefficients.
NOTE: The IIS option is called.
Objective
Phase Iteration Value
1 1 0
NOTE: The IIS option found the problem to be feasible.
NOTE: The OPTLP presolver value AUTOMATIC is applied.
NOTE: The OPTLP presolver removed 0 variables and 0 constraints.
NOTE: The OPTLP presolver removed 0 constraint coefficients.
NOTE: The presolved problem has 3 variables, 3 constraints, and 6 constraint
coefficients.
NOTE: The DUAL SIMPLEX solver is called.
Objective
Phase Iteration Value
2 1 10.000000
NOTE: Optimal.
NOTE: Objective = 10.
NOTE: The data set WORK.EXSS has 12 observations and 3 variables.
NOTE: The data set WORK.PO has 3 observations and 10 variables.

The solution summary and the primal solution are displayed in Output 17.7.4.

Output 17.7.4 Infeasibility Removed

Solution Summary

Obs	Label1	cValue1	nValue1
1	Solver	Dual simplex	.
2	Objective Function	cost	.
3	Solution Status	Optimal	.
4	Objective Value	10	10.000000
5			.
6	Primal Infeasibility	0	0
7	Dual Infeasibility	0	0
8	Bound Infeasibility	0	0
9			.
10	Iterations	1	1.000000
11	Presolve Time	0.00	0
12	Solution Time	0.00	0

Primal Solution

Obs	Objective Function ID	RHS ID	Variable Name	Variable Type	Objective Coefficient	Upper Bound	Variable Value	Variable Status	Reduced Cost
1	cost	rhs	x1	N	1	1.7977E308	0	L	0
2	cost	rhs	x2	N	1	1.7977E308	10	B	0
3	cost	rhs	x3	D	1	3	0	L	1

Top of Page