One of the techniques of NLPU (TECH=CGTR) implements a trust-region algorithm. These types of algorithms determine the search direction by solving the following optimization problem:

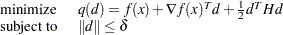Note that the objective function of the preceding problem is a quadratic approximation of the objective function of the original problem. Also the constraint defines a region around which the quadratic function 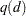is trusted to be an accurate approximation of 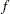. The shape of that region can be thought of as a sphere with radius 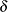. The size of the trust-region radius 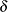is selected based on how well the quadratic function 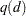approximates the original objective function 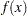. The ratio

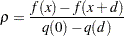defines a measure of how well 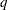approximates 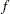within the trust region. If 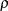is close to , then 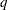is a good approximation of 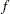and the radius 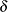is allowed to increase. By letting 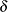increase, the algorithm can take larger steps in subsequent iterations, permitting the algorithm to converge at a faster rate to the optimal solution of the original problem.

On the other hand, if 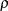is not close to , the quadratic model is considered to be a poor approximation to 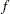for the given trust-region radius. Because the direction is generated with respect to the quadratic model, it is important that a sufficient level of accuracy is maintained between model and objective. In this case, the accuracy of the quadratic model is improved by reducing the trust-region radius 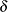. A more in-depth discussion about trust-region methods can be found in Nocedal and Wright (1999).