Previous Page | Next Page

The Unconstrained Nonlinear Programming Solver
Introductory Examples

In this section two introductory examples demonstrate the use of different techniques on different optmization problems.

An Unconstrained Optimization Problem

Consider the following simple purely unconstrained nonlinear problem:

     

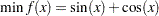You can formulate and solve the problem by using PROC OPTMODEL as follows: 


proc optmodel;
   var x;
   minimize f = sin(x) + cos(x);
   solve with nlpu / tech = lbfgs;
quit;

A problem summary and a solution summary are displayed in Figure 13.2.

Figure 13.2 Optimal Solution of the Example Problem
The OPTMODEL Procedure

Problem Summary
Objective Sense Minimization
Objective Function f
Objective Type Nonlinear
   
Number of Variables 1
Bounded Above 0
Bounded Below 0
Bounded Below and Above 0
Free 1
Fixed 0
   
Number of Constraints 0

Solution Summary
Solver NLPU/LBFGS
Objective Function f
Solution Status Optimal
Objective Value -1.414213562
Iterations 3
   
Optimality Error 2.422204E-12

The iteration log is shown in Figure 13.3.

Figure 13.3 Iteration Log
line
 
NOTE: The problem has 1 variables (1 free, 0 fixed).                            
NOTE: The problem has 0 linear constraints (0 LE, 0 EQ, 0 GE, 0 range).         
NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).      
NOTE: The OPTMODEL presolver removed 0 variables, 0 linear constraints, and 0   
      nonlinear constraints.                                                    
WARNING: No output destinations active.                                         
NOTE: Using analytic derivatives for objective.                                 
NOTE: The Limited Memory BFGS algorithm for unconstrained optimization is       
      called.                                                                   
                     Objective     Optimality   Function                        
           Iter          Value          Error      Calls                        
              0     1.00000000     1.00000000          1                        
              1    -1.36371237     0.10334611          6                        
              2    -1.41421129     0.00075424          9                        
              3    -1.41421356  2.4222035E-12         12                        
NOTE: Optimal.                                                                  
NOTE: Objective = -1.41421356.                                                  
NOTE: At least one W.D format was too small for the number to be printed. The   
      decimal may be shifted by the "BEST" format.                              
 
 

A Bound-Constrained Optimization Problem

Consider the following bound constrained optimization problem:

     

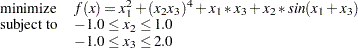As can be seen, there are three variables in this problem. The last two variables are restricted to the specified intervals. For example, the variable can take only values that belong to the interval . These type of restrictions place bounds on the values that the variables can take and are commonly referred to as bound constraints. Optimization problems that have only bound constraints are usually called bound-constrained problems. The following statements can be used to solve this problem: 


proc optmodel;
   var x1;
   var x2 >=  - 1.0 <= 1.0;
   var x3 >= 1.0 <= 2.0;
   minimize obj = x1^2  + (x2 * x3)^4  + x1 * x3  + x2 * sin(x1 + x3) + x2;
   solve with NLPU / tech = CGTR;
quit;

Note that the technique CGTR is used because this is the only technique in NLPU that can solve bound-constrained optimization problems. CGTR stands for the conjugate gradient trust-region algorithm that is discussed in more detail later.

The problem summary and solution summary are displayed in Figure 13.4.

Figure 13.4 Optimal Solution of the Example Problem
The OPTMODEL Procedure

Problem Summary
Objective Sense Minimization
Objective Function obj
Objective Type Nonlinear
   
Number of Variables 3
Bounded Above 0
Bounded Below 0
Bounded Below and Above 2
Free 1
Fixed 0
   
Number of Constraints 0

Solution Summary
Solver NLPU/CGTR
Objective Function obj
Solution Status Optimal
Objective Value -1.429306754
Iterations 6
   
Optimality Error 9.908045E-11
Infeasibility 0

The iteration log is shown in Figure 13.5.

Figure 13.5 Iteration Log
line
 
NOTE: The problem has 3 variables (1 free, 0 fixed).                            
NOTE: The problem has 0 linear constraints (0 LE, 0 EQ, 0 GE, 0 range).         
NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).      
NOTE: The OPTMODEL presolver removed 0 variables, 0 linear constraints, and 0   
      nonlinear constraints.                                                    
NOTE: Using analytic derivatives for objective.                                 
NOTE: Using 2 threads for nonlinear evaluation.                                 
NOTE: The Conjugate Gradient Trust Region algorithm for unconstrained           
      optimization is called.                                                   
NOTE: Initial point was changed to be feasible to bounds.                       
                     Objective     Optimality   Function                        
           Iter          Value          Error      Calls                        
              0              0     1.48172457          1                        
              1    -0.66586831     0.96443628          7                        
              2    -1.13033346     0.06889579         15                        
              3    -1.13280073     0.00030576         23                        
              4    -1.13280078 9.902711656E-9         31                        
NOTE: Optimal.                                                                  
NOTE: Objective = -1.13280078.                                                  
NOTE: At least one W.D format was too small for the number to be printed. The   
      decimal may be shifted by the "BEST" format.                              
 
 

Previous Page | Next Page | Top of Page

Copyright © SAS Institute, Inc. All Rights Reserved.