Overview: NLPU Solver

The unconstrained nonlinear programming solver (NLPU) component of the OPTMODEL procedure can be used for solving general unconstrained nonlinear programming (NLP) problems.

Mathematically, an unconstrained nonlinear programming problem can be stated as

where 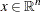is the vector of decision variables and 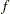: is the nonlinear objective function. 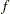is assumed to be twice continuously differentiable, meaning that its second derivatives exist and are continuous in .

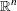For unconstrained optimization problems, PROC OPTMODEL implements the following algorithms:

• Fletcher-Reeves nonlinear conjugate gradient algorithm for convex unconstrained optimization

• Polak-Ribière nonlinear conjugate gradient algorithm for convex unconstrained optimization

• Limited-memory Broyden-Fletcher-Goldfarb-Shanno algorithm for general nonconvex unconstrained optimization (default)

• Conjugate-gradient trust region algorithm for general nonconvex bound-constrained optimization problems

If the objective function is convex, then the optimal solution is a global optimum; otherwise, it is a local optimum. This implies that the optimal solution obtained by the NLPU solver can depend on the starting point. An example of a nonlinear function with multiple local optima is displayed in Figure 13.1.

Figure 13.1 An Example of Multiple Local Optimal Points

The function that is displayed in Figure 13.1 is

where sinc(), also called the "sampling function," is a function that arises frequently in signal processing. The function is defined as