 |
|
| The Mixed Integer Linear Programming Solver |
Example 11.2 Multicommodity Transshipment Problem with Fixed Charges
The following application has been adapted from Example 5.14.
The following example illustrates the use of PROC OPTMODEL to generate a mixed integer linear program to solve a multicommodity network flow model with fixed charges. Consider a network with nodes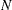 
, arcs 
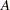, and a set 
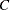of commodities to be shipped between the nodes. There is a variable shipping cost 
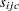for each of the four commodities 
across each of the arcs 
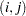. In addition, there is a fixed charge 
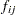for the use of each arc 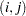. The shipping costs and fixed charges are defined in the data set arcdata, as follows:
data arcdata; array c c1-c4; input from $ to $ c1 c2 c3 c4 fx; datalines; farm-a Chicago 20 15 17 22 100 farm-b Chicago 15 15 15 30 75 farm-c Chicago 30 30 10 10 100 farm-a StLouis 30 25 27 22 150 farm-c StLouis 10 9 11 10 75 Chicago NY 75 75 75 75 200 StLouis NY 80 80 80 80 200 ; run;
The supply (positive numbers) at each of the nodes and the demand (negative numbers) at each of the nodes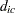 
for each commodity are shown in the data set nodedata, as follows:
data nodedata; array sd sd1-sd4; input node $ sd1 sd2 sd3 sd4; datalines; farm-a 100 100 40 . farm-b 100 200 50 50 farm-c 40 100 75 100 NY -150 -200 -50 -75 ; run;
Let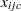 
define the flow of commodity across arc 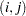. Let 
if arc 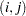is used, and 0 otherwise. Since the total flow on an arc 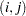must be less than the total demand across all nodes 
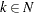, we can define the trivial upper bound 
as
 |
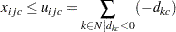This model can be represented using the following mixed integer linear program:
 |
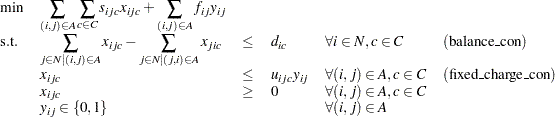Constraint (balance_con) ensures conservation of flow for both supply and demand. Constraint (fixed_charge_con) models the fixed charge cost by forcing if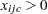 
for any commodity 
.
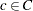The PROC OPTMODEL code follows.
proc optmodel presolver=none;
title ' ';
set COMMODITIES = 1..4;
set <str,str> ARCS;
set <str> NODES = (setof {<i,j> in ARCS} i)
union (setof {<i,j> in ARCS} j);
num shipping_cost {ARCS, COMMODITIES};
num fixed_charge {ARCS};
num supply_demand {NODES, COMMODITIES} init 0;
num upper_bound {ARCS, comm in COMMODITIES} init
sum {i in NODES: supply_demand[i,comm] < 0} (-supply_demand[i,comm]);
read data arcdata into ARCS=[from to] {comm in COMMODITIES}
<shipping_cost[from,to,comm] = col("c"||comm)> fixed_charge=fx;
read data nodedata nomiss into [node] {comm in COMMODITIES}
<supply_demand[node,comm] = col("sd"||comm)>;
var Flow {<i,j> in ARCS, comm in COMMODITIES} >= 0 <= upper_bound[i,j,comm];
var UseArc {ARCS} binary;
/* minimize shipping costs plus fixed charges */
min TotalCost =
sum {<i,j> in ARCS, comm in COMMODITIES}
shipping_cost[i,j,comm] * Flow[i,j,comm]
+ sum {<i,j> in ARCS} fixed_charge[i,j] * UseArc[i,j];
/* flow balance constraints: outflow - inflow <= supply_demand */
con balance_con {i in NODES, comm in COMMODITIES}:
sum {j in NODES: <i,j> in ARCS} Flow[i,j,comm]
- sum {j in NODES: <j,i> in ARCS} Flow[j,i,comm]
<= supply_demand[i,comm];
/* fixed charge constraints: if Flow > 0 for some commodity
then UseArc = 1 */
con fixed_charge_con {<i,j> in ARCS, comm in COMMODITIES}:
Flow[i,j,comm] <= upper_bound[i,j,comm] * UseArc[i,j];
solve with milp;
print {<i,j> in ARCS, comm in COMMODITIES: Flow[i,j,comm] > 1.0e-5} Flow;
for {<i,j> in ARCS} UseArc[i,j] = round(UseArc[i,j].sol);
print UseArc;
quit;
The solution summary, as well as the output from the two PRINT statements, are shown in Output 11.2.1.
| Problem Summary | |
|---|---|
| Objective Sense | Minimization |
| Objective Function | TotalCost |
| Objective Type | Linear |
| Number of Variables | 35 |
| Bounded Above | 0 |
| Bounded Below | 0 |
| Bounded Below and Above | 35 |
| Free | 0 |
| Fixed | 0 |
| Binary | 7 |
| Integer | 0 |
| Number of Constraints | 52 |
| Linear LE (<=) | 52 |
| Linear EQ (=) | 0 |
| Linear GE (>=) | 0 |
| Linear Range | 0 |
| Solution Summary | |
|---|---|
| Solver | MILP |
| Objective Function | TotalCost |
| Solution Status | Optimal |
| Objective Value | 42825 |
| Iterations | 23 |
| Best Bound | . |
| Nodes | 1 |
| Relative Gap | 0 |
| Absolute Gap | 0 |
| Primal Infeasibility | 0 |
| Bound Infeasibility | 0 |
| Integer Infeasibility | 0 |
|
|
Copyright © SAS Institute, Inc. All Rights Reserved.