| The NLPC Nonlinear Optimization Solver |
Example 12.3 Simple Pooling Problem
Consider Example 6.7 in the PROC NLP documentation. In this simple pooling problem, two liquid chemicals,  and
and  , are produced by the pooling and blending of three input liquid chemicals,
, are produced by the pooling and blending of three input liquid chemicals,  ,
, 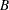 , and
, and  . There are three group of constraints: 1) the mass balance constraints, which are linear constraints; 2) the sulfur concentration constraints, which are nonlinear constraints; and 3) the bound constraints. The objective is to maximize the profit.
. There are three group of constraints: 1) the mass balance constraints, which are linear constraints; 2) the sulfur concentration constraints, which are nonlinear constraints; and 3) the bound constraints. The objective is to maximize the profit.
You can formulate this problem in PROC OPTMODEL as follows:
proc optmodel;
num costa = 6, costb = 16, costc = 10,
costx = 9, costy = 15;
var amountx init 1 >= 0 <= 100,
amounty init 1 >= 0 <= 200;
var amounta init 1 >= 0,
amountb init 1 >= 0,
amountc init 1 >= 0;
var pooltox init 1 >= 0,
pooltoy init 1 >= 0;
var ctox init 1 >= 0,
ctoy init 1 >= 0;
var pools init 1 >=1 <= 3;
max f = costx*amountx + costy*amounty
- costa*amounta - costb*amountb - costc*amountc;
con mb1: amounta + amountb = pooltox + pooltoy,
mb2: pooltox + ctox = amountx,
mb3: pooltoy + ctoy = amounty,
mb4: ctox + ctoy = amountc;
con sc1: 2.5*amountx - pools*pooltox - 2*ctox >= 0,
sc2: 1.5*amounty - pools*pooltoy - 2*ctoy >= 0,
sc3: 3*amounta + amountb - pools*(amounta + amountb) = 0;
solve with nlpc / tech=quanew printfreq=1;
print amountx amounty amounta amountb amountc;
quit;
The quantities amounta, amountb, amountc, amountx, and amounty are the amounts to be determined for the liquid chemicals  ,
, 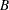 ,
,  ,
,  , and
, and  , respectively. pooltox, pooltoy, ctox, ctoy, and pools are intermediate decision variables, whose values are not printed in the solution. The constraints mb1–mb4 are the mass balance constraints, and the constraints sc1–sc3 are the sulfur concentration constraints. For more information about converting PROC NLP models into PROC OPTMODEL models, see the section Rewriting NLP Models for PROC OPTMODEL.
, respectively. pooltox, pooltoy, ctox, ctoy, and pools are intermediate decision variables, whose values are not printed in the solution. The constraints mb1–mb4 are the mass balance constraints, and the constraints sc1–sc3 are the sulfur concentration constraints. For more information about converting PROC NLP models into PROC OPTMODEL models, see the section Rewriting NLP Models for PROC OPTMODEL.
To solve the optimization problem, the experimental quasi-Newton method (QUANEW) is invoked. The problem summary is shown in Output 12.3.1. Output 12.3.2 displays the iteration log.
| Problem Summary | |
|---|---|
| Objective Sense | Maximization |
| Objective Function | f |
| Objective Type | Linear |
| Number of Variables | 10 |
| Bounded Above | 0 |
| Bounded Below | 7 |
| Bounded Below and Above | 3 |
| Free | 0 |
| Fixed | 0 |
| Number of Constraints | 7 |
| Linear LE (<=) | 0 |
| Linear EQ (=) | 4 |
| Linear GE (>=) | 0 |
| Linear Range | 0 |
| Nonlinear LE (<=) | 0 |
| Nonlinear EQ (=) | 1 |
| Nonlinear GE (>=) | 2 |
| Nonlinear Range | 0 |
| Iteration Log: Quasi-Newton Method with BFGS Update | ||||||
|---|---|---|---|---|---|---|
| Iter | Function Calls |
Objective Value |
Infeasibility | Optimality Error |
Step Size |
Predicted Function Reduction |
| 0 | 0 | 3.8182 | 0.6818 | 0.0527 | . | . |
| 1 | 1 | -2.6893 | 0.1731 | 0.2383 | 1.000 | 3.0428 |
| 2 | 2 | -1.9376 | 0.0709 | 0.2202 | 1.000 | 4.6944 |
| 3 | 3 | 1.2603 | 0.0541 | 0.0566 | 1.000 | 1.5883 |
| 4 | 4 | 2.4293 | 0.008492 | 0.4107 | 1.000 | 1.1871 |
| 5 | 5 | 3.2903 | 2.107E-10 | 0.1666 | 1.000 | 2.5714 |
| 6 | 6 | 5.0987 | 3.161E-10 | 0.3283 | 1.000 | 4.9682 |
| 7 | 7 | 10.0669 | 2.107E-10 | 2.6895 | 1.000 | 63.9047 |
| 8 | 9 | 28.3332 | 0.4785 | 8.3364 | 0.286 | 115.6 |
| 9 | 10 | 103.3932 | 2.0648 | 31.3704 | 1.000 | 112.7 |
| 10 | 11 | 159.4438 | 1.421E-14 | 11.7888 | 1.000 | 376.4 |
| 11 | 12 | 398.1735 | 2.2676 | 9.4167 | 1.000 | 29.8946 |
| 12 | 13 | 397.8877 | 0.006033 | 0.8947 | 1.000 | 0.0901 |
| 13 | 14 | 397.9164 | 5.9666E-6 | 0.9195 | 1.000 | 0.2738 |
| 14 | 15 | 398.1901 | 0.000719 | 0.6228 | 1.000 | 2.4290 |
| 15 | 16 | 400.0000 | 0.0316 | 0.0123 | 1.000 | 0.3795 |
| 16 | 17 | 400.0000 | 7.5712E-7 | 1.8714E-8 | 1.000 | 9.867E-6 |
| Note: | Optimality criteria (ABSOPTTOL=0.001, OPTTOL=1E-6) are satisfied. |
Output 12.3.3 displays the solution summary and the solution. The optimal solution shows that to obtain a maximum profit of 400, 200 units of  should be produced by blending 100 units of
should be produced by blending 100 units of 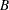 and 100 units of
and 100 units of  . Liquid
. Liquid  should not be used for the blending. Further, liquid
should not be used for the blending. Further, liquid  should not be produced at all.
should not be produced at all.
Copyright © SAS Institute, Inc. All Rights Reserved.