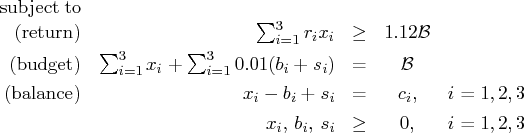The Quadratic Programming Solver: Example 12.3: Portfolio Selection with Transactions :: SAS/OR(R) 9.2 User's Guide: Mathematical Programming

The Quadratic Programming Solver -- Experimental

Example 12.3: Portfolio Selection with Transactions

Consider a portfolio selection problem with a slight modification. You are now required to take into account the current position and transaction costs associated with buying and selling assets. The objective is to find the minimum variance portfolio. In order to understand the scenario better, consider the following data.

You are given three assets. The current holding of the three assets is denoted by the vector $\mathbf{c}$ = [200, 300, 500], the amount of asset bought and sold is denoted by and , respectively, and the net investment in each asset is denoted by and is defined by the following relation:

$x_i - b_i + s_i = c_i, \;\; i = 1, 2, 3$

Let us say that you pay a transaction fee of 0.01 every time you buy or sell. Let the covariance matrix $\mathcal{c}$ be defined as

$\mathcal{c} & = & [ 0.027489 & -0.00874 & -0.00015 \ -0.00874 & 0.109449 & -0.00012 \ -0.00015 & -0.00012 & 0.000766 \ ]\$

Assume that you hope to obtain at least 12% growth. Let $\mathbf{r}$ = [1.109048, 1.169048, 1.074286] be the vector of expected return on the three assets, and let $\mathcal{b}$ =1000 be the available funds. Mathematically, this problem can be written in the following manner:

${\min} & 0.027489x_1^2 - 0.01748 x_1 x_2 - 0.0003 x_1 x_3 + 0.109449x_2^2 \ & - 0.00024 x_2 x_3 + 0.000766 x_3^2 \$

${\rm subjectto} & & & & \ ({\rm return}) & \sum_{i=1}^3 r_i x_i & \geq & 1.12 ... ...+ s_i & = & c_i, & i = 1, 2, 3 \ & x_i,\,b_i,\,s_i & \ge & 0, & i = 1, 2, 3 \$

The problem can be solved by the following SAS code:

    /* example 3: portfolio selection with transactions */
    proc optmodel;
       /* let x1, x2, x3 be the amount invested in each asset */
       var x{1..3} >= 0;
       /* let b1, b2, b3 be the amount of asset bought */
       var b{1..3} >= 0;
       /* let s1, s2, s3 be the amount of asset sold */
       var s{1..3} >= 0;
       
       /* current holdings */
       num c{1..3}=[ 200 300 500];
       /* covariance matrix */
       num coeff{1..3, 1..3} = [0.027489  -.008740  -.000150
                                -.008740  0.109449  -.000120
                                -.000150  -.000120  0.000766];
       /* returns */
       num r{1..3}=[1.109048 1.169048 1.074286];
       
       /* minimize the variance of the portfolio's total return */
       minimize f = sum{i in 1..3, j in 1..3}coeff[i,j]*x[i]*x[j];
       
       /* subject to the following constraints */
       con BUDGET: sum{i in 1..3}(x[i]+.01*b[i]+.01*s[i]) <= 1000;
       con RETURN: sum{i in 1..3}r[i]*x[i] >= 1120;
       con BALANC{i in 1..3}: x[i]-b[i]+s[i]=c[i];
       
       solve with qp;
       
       /* print the optimal solution */
       print x;
    quit;

The output is displayed in Output 12.3.1.

Output 12.3.1: Portfolio Selection with Transactions

The OPTMODEL Procedure

Problem Summary
Objective Sense	Minimization
Objective Function	f
Objective Type	Quadratic

Number of Variables	9
Bounded Above	0
Bounded Below	9
Bounded Below and Above	0
Free	0
Fixed	0

Number of Constraints	5
Linear LE (<=)	1
Linear EQ (=)	3
Linear GE (>=)	1
Linear Range	0

The OPTMODEL Procedure

Solution Summary
Solver	QP
Objective Function	f
Solution Status	Optimal
Objective Value	19560.725967
Iterations	17

Primal Infeasibility	4.506349E-15
Dual Infeasibility	0
Bound Infeasibility	0
Duality Gap	5.8692616E-8
Complementarity	0.0011480356

[1]	x
1	397.58
2	406.12
3	190.17

Top of Page