PROC OPTQP: PROC OPTQP Statement :: SAS/OR(R) 9.2 User's Guide: Mathematical Programming

The OPTQP Procedure

PROC OPTQP Statement

The following options can be specified in the PROC OPTQP statement.

DATA=SAS-data-set: specifies the input SAS data set. This data set can also be created from a QPS-format flat file by using the SAS macro %MPS2SASD. If the DATA= option is not specified, PROC OPTQP will use the most recently created SAS data set. See Chapter 14, "The MPS-Format SAS Data Set," for more details.

DUALOUT=SAS-data-set

DOUT=SAS-data-set

specifies the output data set containing the dual solution. See the section "Output Data Sets" for details.

MAXITER=

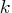
specifies the maximum number of predictor-corrector iterations performed by the interior point algorithm (see the section "Interior Point Algorithm: Overview"). The value

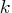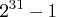is an integer between 1 and the largest four-byte, signed integer, which is $2^{31} - 1$ . If you do not specify this option, the procedure does not stop based on the number of iterations performed.

MAXTIME=

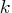
specifies an upper limit of

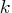seconds of real time for reading in the data and performing the optimization process. If you do not specify this option, the procedure does not stop based on the amount of time elapsed.

OBJSENSE=option

specifies whether the QP model is a minimization or a maximization problem. You specify OBJSENSE=MIN for a minimization problem and OBJSENSE=MAX for a maximization problem. Alternatively, you can specify the objective sense in the input data set; see the section "ROWS Section" for details. If for some reason the objective sense is specified differently in these two places, this option supersedes the objective sense specified in the input data set. If the objective sense is not specified anywhere, then PROC OPTQP interprets and solves the quadratic program as a minimization problem.

PRESOLVER=option

PRESOL=option

specifies one of the following presolve options:

Option	Description
NONE (0)	Disable presolver.
AUTOMATIC (-1)	Apply presolver by using default setting.
BASIC (1)	Apply basic presolver.
MODERATE (2)	Apply moderate presolver.
AGGRESSIVE (3)	Apply aggressive presolver.

You can also specify the option by integers from -1 to 3. The integer value for each option is indicated in parentheses. The default option is AUTOMATIC.

PRIMALOUT=SAS-data-set

POUT=SAS-data-set

specifies the output data set containing the primal solution. See the section "Output Data Sets" for details.

PRINTFREQ=

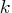
specifies that the printing of the solution progress to the iteration log should occur after every

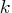iterations. The print frequency,

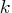, is an integer between zero and the largest four-byte, signed integer, which is 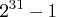$2^{31} - 1$ . The value

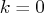disables the printing of the progress of the solution. The default value of this option is 1.

PRINTLEVEL=0 1

specifies whether a summary of the problem and solution should be printed. If PRINTLEVEL=1, then two ODS (Output Delivery System) tables named "ProblemSummary" and "SolutionSummary" are produced and printed. If PRINTLEVEL=0, then no ODS tables are produced or printed. The default value of this option is 1.

For details about the ODS tables created by PROC OPTQP, see the section "ODS Tables".

SAVE_ONLY_IF_OPTIMAL

specifies that the PRIMALOUT= and DUALOUT= data sets be saved only if the final solution obtained by the solver at termination is optimal. If the PRIMALOUT= or DUALOUT= option is specified, and this option is not specified, then the output data sets will only contain solution values at optimality. If the SAVE_ONLY_IF_OPTIMAL option is not specified, the output data sets will not contain an intermediate solution.

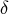
STOP_DG= $\delta$

specifies the desired relative duality gap, 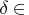$\delta \in$ [1E - 9, 1E - 4]. This is the relative difference between the primal and dual objective function values and is the primary solution quality parameter. The default value is 1E - 6. See the section "Interior Point Algorithm: Overview" for details.

STOP_DI= $\beta$

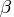
specifies the maximum allowed relative dual constraints violation, 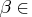$\beta \in$ [1E - 9, 1E - 4]. The default value is 1E - 6. See the section "Interior Point Algorithm: Overview" for details.

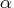
STOP_PI= $\alpha$

specifies the maximum allowed relative bound and primal constraints violation, 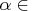$\alpha \in$ [1E - 9, 1E - 4]. The default value is 1E - 6. See the section "Interior Point Algorithm: Overview" for details.

Top of Page