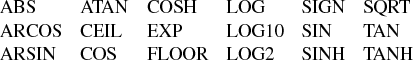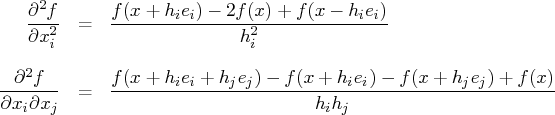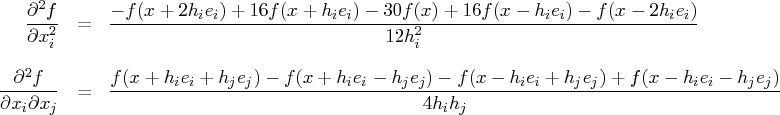PROC OPTMODEL: Automatic Differentiation :: SAS/OR(R) 9.2 User's Guide: Mathematical Programming

The OPTMODEL Procedure

Automatic Differentiation

PROC OPTMODEL automatically generates code to evaluate the derivatives for most objective expressions and nonlinear constraints. PROC OPTMODEL generates analytic derivatives for objective and constraint expressions written in terms of the procedure's mathematical operators and the following functions:

$\textrm{abs} & \textrm{atan} & \textrm{cosh} & \textrm{log} & \textrm{sign} & \t... ...\textrm{cos} & \textrm{floor} & \textrm{log2} & \textrm{sinh} & \textrm{tanh} \$

CAUTION: Some of these functions, such as ABS, FLOOR, and SIGN, as well as some operators, such as IF-THEN, <> (element minimum operator), and >< (element maximum operator), must be used carefully in modeling expressions because functions including such components are not continuously differentiable or even continuous.

Expressions that use other SAS library functions might require numerical approximation of derivatives. PROC OPTMODEL uses either forward-difference approximation or central-difference approximation as specified by the FD= option (see the section "PROC OPTMODEL Statement").

Note: The numerical gradient approximations are significantly slower than automatically generated derivatives when there are a large number of optimization variables.

Forward-Difference Approximations

The FD=FORWARD option requests the use of forward-difference derivative approximations. For a function

variables, the first-order derivatives are approximated by

$g_i = {\partial f \over \partial x_i} = {f( x + e_i{}h_i ) - f( x ) \over h_i}$

Notice that additional function calls are needed here. The step lengths , , are based on the assumed function precision, DIGITS:

$h_i = 10^{-{digits}/2} (1 + | x_i|)$

You can use the FDIGITS= option to specify the function precision, DIGITS, for the objective function. For constraints, use the CDIGITS= option.

The second-order derivatives are approximated using extra function calls (Dennis and Schnabel 1983, pp. 80, 104):

$\frac{\partial^2 f}{\partial x^2_i} & = & \frac{f(x + h_ie_i) - 2f(x) + f(x - ... ...j} & = & \frac{f(x+h_ie_i+h_je_j) - f(x+h_ie_i) - f(x+h_je_j) + f(x)}{h_ih_j}$

Notice that the diagonal of the Hessian uses a central-difference approximation (Abramowitz and Stegun 1972, p. 884). The step lengths are

$h_i = 10^{-{digits}/3} (1 + | x_i|)$

Central-Difference Approximations

The FD=CENTRAL option requests the use of central-difference derivative approximations. Generally, central-difference approximations are more accurate than forward-difference approximations, but they require more function evaluations. For a function

variables, the first-order derivatives are approximated by

$g_i = {\partial f \over \partial x_i} = {f( x + e_i{}h_i ) - f( x - e_i{}h_i ) \over 2{}h_i}$

Notice that additional function calls are needed here. The step lengths , , are based on the assumed function precision, DIGITS:

$h_i = 10^{-{digits}/3} (1 + | x_i|)$

You can use the FDIGITS= option to specify the function precision, DIGITS, for the objective function. For constraints, use the CDIGITS= option.

The second-order derivatives are approximated using extra function calls (Abramowitz and Stegun 1972, p. 884):

$\frac{\partial^2 f}{\partial x^2_i} & = & \frac{-f(x + 2h_ie_i) + 16f(x + h_ie... ..._j) - f(x+h_ie_i-h_je_j) - f(x-h_ie_i+h_je_j) + f(x-h_ie_i-h_je_j)}{4h_ih_j}$

The step lengths are

$h_i = 10^{-{digits}/3} (1 + | x_i|)$

Top of Page