The OPTMODEL Procedure

VAR Declaration

VAR var-decl [, ...var-decl];

The VAR statement declares one or more optimization variables. Multiple VAR statements are permitted. A variable is not allowed to have the same name as a parameter or constraint.

Each var-decl specifies a variable name. The name can be followed by an array index-set specification and then variable options. Dummy parameters declared in the index set specification can be used in the following variable options.

Here is the syntax for a var-decl:

name [ { index-set } ] [ var-option(s) ]

For example, the following code declares a group of 100 variables, x[1]--x[100]:

  
    proc optmodel; 
       var x{1..100};
 

Here are the available variable options:

INIT expression

sets an initial value for the variable. The expression is used only the first time the value is required. If no initial value is specified, then 0 is used by default.

>= expression

sets a lower bound for the variable value. The default lower bound is .

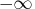<= expression

sets an upper bound for the variable value. The default upper bound is .

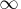INTEGER

requests that the solver assign the variable an integer value.

BINARY

requests that the solver assign the variable a value of either 0 or 1.

For example, the following code declares a variable that has an initial value of 0.5. The variable is bounded between 0 and 1:

  
    proc optmodel; 
       var x init 0.5 >= 0 <= 1;
 

The values of the bounds can be determined later by using suffixed references to the variable. For example, the upper bound for variable x can be referred to as x.ub. In addition the bounds options can be overridden by explicit assignment to the suffixed variable name. Suffixes are described further in the section "Suffixes".

When used in an expression, an unsuffixed variable name refers to the current value of the variable. Unsuffixed variables are not allowed in the expressions for options that define variable bounds or initial values. Such expressions have values that must be fixed during execution of the solver.