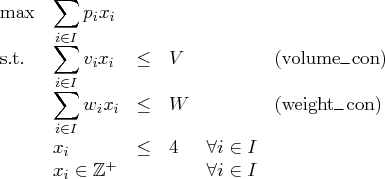PROC OPTMILP: Example 16.1: Simple Integer Linear Program :: SAS/OR(R) 9.2 User's Guide: Mathematical Programming

The OPTMILP Procedure

Example 16.1: Simple Integer Linear Program

This example illustrates a model in an MPS-format SAS data set. This data set is passed to PROC OPTMILP and a solution is found.

Consider a scenario where you have a container with a set of limiting attributes (volume and weight ) and a set of items that you want to pack. Each item type has a certain value , a volume , and a weight . You must choose at most four items of each type so that the total value is maximized and all the chosen items fit into the container. Let be the number of items of type to be included in the container. This model can be formulated as the following integer linear program:

$\max & \displaystyle\sum_{i \in i} p_i x_i & \ {\rm s.t.} & \displaystyle\sum_{... ...& \leq & 4 & \forall i \in i\ & x_i \in \mathbb{z}^{+} & & & \forall i \in i\$

Constraint (volume_con) enforces the volume capacity limit, while constraint (weight_con) enforces the weight capacity limit. An instance of this problem can be saved in an MPS-format SAS data set by using the following code:

  
    data ex1data; 
       input field1 $ field2 $ field3 $ field4 field5 $ field6; 
       datalines; 
    NAME                     ex1data           .                       . 
    ROWS                                       .                       . 
    MAX        z                               .                       . 
    L          volume_con                      .                       . 
    L          weight_con                      .                       . 
    COLUMNS                                    .                       . 
               .MRK0         'MARKER'          .     'INTORG'          . 
               x[1]          z                 1     volume_con       10 
               x[1]          weight_con       12                       . 
               x[2]          z                 2     volume_con      300 
               x[2]          weight_con       15                       . 
               x[3]          z                 3     volume_con      250 
               x[3]          weight_con       72                       . 
               x[4]          z                 4     volume_con      610 
               x[4]          weight_con      100                       . 
               x[5]          z                 5     volume_con      500 
               x[5]          weight_con      223                       . 
               x[6]          z                 6     volume_con      120 
               x[6]          weight_con       16                       . 
               x[7]          z                 7     volume_con       45 
               x[7]          weight_con       73                       . 
               x[8]          z                 8     volume_con      100 
               x[8]          weight_con       12                       . 
               x[9]          z                 9     volume_con      200 
               x[9]          weight_con      200                       . 
               x[10]         z                10     volume_con       61 
               x[10]         weight_con      110                       . 
               .MRK1         'MARKER'          .     'INTEND'          . 
    RHS                                        .                       . 
               .RHS.         volume_con     1000                       . 
               .RHS.         weight_con      500                       . 
    BOUNDS                                     .                       . 
    UP         .BOUNDS.      x[1]              4                       . 
    UP         .BOUNDS.      x[2]              4                       . 
    UP         .BOUNDS.      x[3]              4                       . 
    UP         .BOUNDS.      x[4]              4                       . 
    UP         .BOUNDS.      x[5]              4                       . 
    UP         .BOUNDS.      x[6]              4                       . 
    UP         .BOUNDS.      x[7]              4                       . 
    UP         .BOUNDS.      x[8]              4                       . 
    UP         .BOUNDS.      x[9]              4                       . 
    UP         .BOUNDS.      x[10]             4                       . 
    ENDATA                                     .                       . 
    ;

In the COLUMNS section of this data set, the name of the objective is z, and the objective coefficients appear in field4. The coefficients of (volume_con) appear in field6. The coefficients of (weight_con) appear in field4. In the RHS section, the bounds and appear in field4.

This problem can be solved by using the following statement to call the OPTMILP procedure:

    proc optmilp data=ex1data primalout=ex1soln;
    run;

The progress of the solver is shown in Output 16.1.1.

Output 16.1.1: Simple Integer Linear Program PROC OPTMILP Log



NOTE: The problem ex1data has 10 variables (0 binary, 10 integer, 0 free, 0
fixed).
NOTE: The problem has 2 constraints (2 LE, 0 EQ, 0 GE, 0 range).
NOTE: The problem has 20 constraint coefficients.
NOTE: The OPTMILP presolver value AUTOMATIC is applied.
NOTE: The OPTMILP presolver removed 0 variables and 0 constraints.
NOTE: The OPTMILP presolver removed 0 constraint coefficients.
NOTE: The OPTMILP presolver modified 0 constraint coefficients.
NOTE: The presolved problem has 10 variables, 2 constraints, and 20 constraint
coefficients.
NOTE: The MIXED INTEGER LINEAR solver is called.
Node Active Sols BestInteger BestBound Gap Time
0 1 1 0 88.0955497 100.00% 0
0 1 2 83.0000000 88.0626822 5.75% 0
0 1 2 83.0000000 87.9665871 5.65% 0
0 1 2 83.0000000 87.9660825 5.65% 0
0 1 3 85.0000000 87.9331742 3.34% 0
0 1 3 85.0000000 87.9140538 3.31% 0
NOTE: OPTMILP added 3 cuts with 30 cut coefficients at the root.
5 2 4 86.0000000 87.6821242 1.92% 0
8 0 5 87.0000000 . 0.00% 0
NOTE: Optimal.
NOTE: Objective = 87.
NOTE: The data set WORK.EX1SOLN has 10 observations and 8 variables.
NOTE: PROCEDURE OPTMILP used (Total process time):
real time 0.03 seconds
cpu time 0.03 seconds

The data set ex1soln is shown in Output 16.1.2.

Output 16.1.2: Simple Integer Linear Program Solution

Example 1 Solution Data

Objective Function ID	RHS ID	Variable Name	Variable Type	Objective Coefficient	Upper Bound	Variable Value
z	.RHS.	x[1]	I	1	4	0
z	.RHS.	x[2]	I	2	4	0
z	.RHS.	x[3]	I	3	4	0
z	.RHS.	x[4]	I	4	4	0
z	.RHS.	x[5]	I	5	4	0
z	.RHS.	x[6]	I	6	4	3
z	.RHS.	x[7]	I	7	4	1
z	.RHS.	x[8]	I	8	4	4
z	.RHS.	x[9]	I	9	4	0
z	.RHS.	x[10]	I	10	4	3

The optimal solution is , and $x_{10} = 3$ , with a total value of 87. From this solution, you can compute the total volume used, which is 988 ( $\leq v = 1000$ ); the total weight used is 499 ( $\leq w = 500$ ). The problem summary and solution summary are shown in Output 16.1.3.

Output 16.1.3: Simple Integer Linear Program Summary

Problem Summary
Problem Name	ex1data
Objective Sense	Maximization
Objective Function	z
RHS	.RHS.

Number of Variables	10
Bounded Above	0
Bounded Below	0
Bounded Above and Below	10
Free	0
Fixed	0
Binary	0
Integer	10

Number of Constraints	2
LE (<=)	2
EQ (=)	0
GE (>=)	0
Range	0

Constraint Coefficients	20

Solution Summary
Objective Function	z
Solution Status	Optimal
Objective Value	87

Relative Gap	0
Absolute Gap	0
Primal Infeasibility	0
Bound Infeasibility	0
Integer Infeasibility	0

Best Bound	.
Nodes	9
Iterations	34
Presolve Time	0.00
Solution Time	0.00

Top of Page