| The Unconstrained Nonlinear Programming Solver |
Conditions of Optimality
Before beginning the discussion, we present the following notation for easy reference:
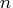
- dimension of
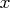 , i.e., the number of decision variables
, i.e., the number of decision variables
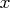
- iterate, i.e., the vector of
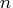 decision variables
decision variables
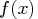
- objective function
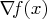
- gradient of the objective function
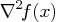
- Hessian matrix of the objective function
A point ![]() is a local solution of the problem if there exists a
neighborhood
is a local solution of the problem if there exists a
neighborhood ![]() of
of ![]() such that
such that
All the algorithms in the NLPU solver find a local minimum of an optimization problem.
Unconstrained Optimization
The following conditions hold for unconstrained optimization problems:- First-order necessary conditions: If
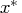 is a local solution and
is a local solution and 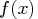 is
continuously differentiable in some neighborhood of
is
continuously differentiable in some neighborhood of 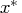 , then
, then
- Second-order necessary conditions: If
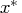 is a local solution and
is a local solution and 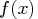 is twice continuously differentiable in some neighborhood of
is twice continuously differentiable in some neighborhood of 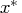 , then
, then
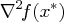 is positive semidefinite.
is positive semidefinite.
- Second-order sufficient conditions: If
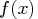 is twice continuously differentiable in some neighborhood of
is twice continuously differentiable in some neighborhood of 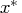 , and
, and
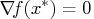 and
and 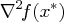 is positive definite, then
is positive definite, then 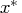 is a
strict local solution.
is a
strict local solution.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.