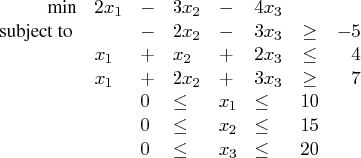PROC NETFLOW: Example 5.15: Converting to an MPS-Format SAS Data Set :: SAS/OR(R) 9.2 User's Guide: Mathematical Programming

The NETFLOW Procedure

Example 5.15: Converting to an MPS-Format SAS Data Set

This example demonstrates the use of the MPSOUT= option to convert a problem data set in PROC NETFLOW input format into an MPS-format SAS data set for use with the OPTLP procedure.

Suppose you want to solve a linear program with the following formulation:

${min} & 2x_1 & - & 3x_2 & - & 4x_3 & & \ { subject to } & & - & 2x_2 & - & 3x_3... ...0 & \ & & 0 & \leq & x_2 & \leq & 15 & \ & & 0 & \leq & x_3 & \leq & 20 & \$

You can save the LP in dense format by using the following DATA step:

 data exdata;
    input x1 x2 x3 _type_ $ _rhs_;
 datalines;
 2 -3 -4 min      .
 . -2 -3 >=      -5
 1  1  2 <=       6
 1  2  3 >=       7
 10 15 20 upperbd  .
 ;

If you decide to solve the problem by using the OPTLP procedure, you need to convert the data set exdata from dense format to MPS format. You can accomplish this by using the following statements:

    /* convert to MPS format */
    
    proc netflow condata=exdata mpsout=mpsdata bytes=100000; 
    run;

The MPS-format SAS data set mpsdata is shown in Output 5.15.1.

Output 5.15.1: Data Set mpsdata

Obs	field1	field2	field3	field4	field5	field6
1	NAME		modname	.		.
2	ROWS			.		.
3	MIN	objfn		.		.
4	G	_OBS2_		.		.
5	L	_OBS3_		.		.
6	G	_OBS4_		.		.
7	COLUMNS			.		.
8		x1	objfn	2	_OBS3_	1
9		x1	_OBS4_	1		.
10		x2	objfn	-3	_OBS2_	-2
11		x2	_OBS3_	1	_OBS4_	2
12		x3	objfn	-4	_OBS2_	-3
13		x3	_OBS3_	2	_OBS4_	3
14	RHS			.		.
15			_OBS2_	-5	_OBS3_	6
16			_OBS4_	7		.
17	BOUNDS			.		.
18	UP	bdsvect	x1	10		.
19	UP	bdsvect	x2	15		.
20	UP	bdsvect	x3	20		.
21	ENDATA			.		.

The constraint names _OBS2_, _OBS3_, and _OBS4_ are generated by the NETFLOW procedure. If you want to provide your own constraint names, use the ROW list variable in the CONOUT= data set. If you specify the problem data in sparse format instead of dense format, the MPSOUT= option produces the same MPS-format SAS data set shown in the preceding output.

Now that the problem data is in MPS format, you can solve the problem by using the OPTLP procedure. For more information, see Chapter 15, "The OPTLP Procedure."

Top of Page