The NETFLOW Procedure

Example 5.2: Minimum Cost Flow Problem

You can continue to use the pineapple example in Example 5.1 by supposing that the airlines now stipulate that no more than 350 pineapples per week can be handled in any single leg of the journey. The restaurant uses 500 pineapples each week. How many pineapples should take each route between Hawaii and London?

You will probably have more minimum cost flow problems because they are more general than maximal flow and shortest path problems. A shortest path formulation is no longer valid because the sink node does not demand one flow unit.

All arcs have the same capacity of 350 pineapples. Because of this, the DEFCAPACITY= option can be specified in the PROC NETFLOW statement, rather than having a CAPACITY list variable in ARCDATA=aircost1. You can have a CAPACITY list variable, but the value of this variable would be 350 in all observations, so using the DEFCAPACITY= option is more convenient. You would have to use the CAPACITY list variable if arcs had differing capacities. You can use both the DEFCAPACITY= option and a CAPACITY list variable.

There is only one supply node and one demand node. These can be named in the SOURCE= and SINK= options. DEMAND=500 is specified for the restaurant demand. There is no need to specify SUPPLY=500, as this is assumed.

  
   title 'Minimum Cost Flow Problem'; 
   title2 'How to get Hawaiian Pineapples to a London Restaurant'; 
   proc netflow 
      defcapacity=350 
      sourcenode='Honolulu' 
      sinknode='Heathrow London'  /* Quotes for embedded blank */ 
      demand=500 
         arcdata=aircost1 
         arcout=arcout1 
         nodeout=nodeout1; 
            tail    ffrom; 
            head    tto; 
      set future1; 
   proc print data=arcout1; sum _fcost_; 
   proc print data=nodeout1; 
   run;
 

The following notes appear on the SAS log:

  
   NOTE: SOURCENODE was assigned supply of the total 
         network demand= 500 . 
   NOTE: Number of nodes= 8 . 
   NOTE: Number of supply nodes= 1 . 
   NOTE: Number of demand nodes= 1 . 
   NOTE: Total supply= 500 , total demand= 500 . 
   NOTE: Number of arcs= 13 . 
   NOTE: Number of iterations performed (neglecting any 
         constraints)= 6 . 
   NOTE: Of these, 4 were degenerate. 
   NOTE: Optimum (neglecting any constraints) found. 
   NOTE: Minimal total cost= 93750 . 
   NOTE: The data set WORK.ARCOUT1 has 13 observations and 
         13 variables. 
   NOTE: The data set WORK.NODEOUT1 has 9 observations and 
         10 variables.
 

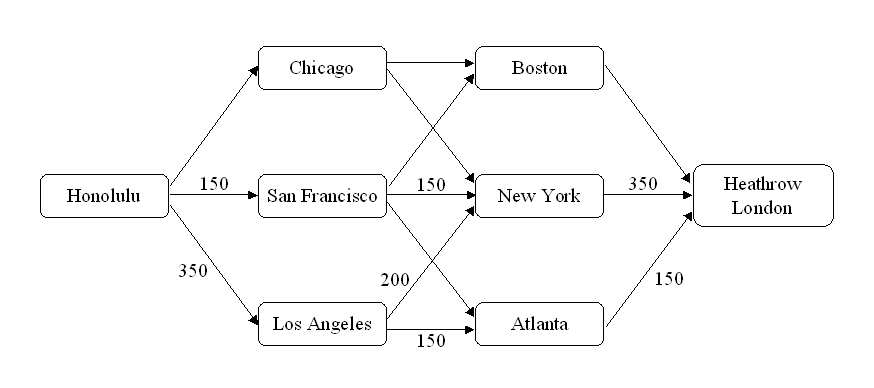
Figure 5.41: Pineapple Routes: Minimum Cost Flow Solution

The routes and numbers of pineapples in each arc can be seen in the output data set ARCOUT=arcout1 in Output 5.2.1. NODEOUT=NODEOUT1 is shown in Output 5.2.2.

Output 5.2.1: ARCOUT=ARCOUT1

Minimum Cost Flow Problem How to get Hawaiian Pineapples to a London Restaurant Obs ffrom tto _cost_ _CAPAC_ _LO_ _SUPPLY_ _DEMAND_ _FLOW_ _FCOST_ _RCOST_ _ANUMB_ _TNUMB_ _STATUS_ 1 San Francisco Atlanta 63 350 0 . . 0 0 2 9 3 LOWERBD NONBASIC 2 Los Angeles Atlanta 57 350 0 . . 150 8550 . 10 4 KEY_ARC BASIC 3 Chicago Boston 45 350 0 . . 0 0 4 4 2 LOWERBD NONBASIC 4 San Francisco Boston 71 350 0 . . 0 0 . 5 3 KEY_ARC BASIC 5 Honolulu Chicago 105 350 0 500 . 0 0 . 1 1 KEY_ARC BASIC 6 Boston Heathrow London 88 350 0 . 500 0 0 22 11 5 LOWERBD NONBASIC 7 New York Heathrow London 65 350 0 . 500 350 22750 -24 12 6 UPPERBD NONBASIC 8 Atlanta Heathrow London 76 350 0 . 500 150 11400 . 13 7 KEY_ARC BASIC 9 Honolulu Los Angeles 68 350 0 500 . 350 23800 -11 3 1 UPPERBD NONBASIC 10 Chicago New York 56 350 0 . . 0 0 38 6 2 LOWERBD NONBASIC 11 San Francisco New York 48 350 0 . . 150 7200 . 7 3 KEY_ARC BASIC 12 Los Angeles New York 44 350 0 . . 200 8800 . 8 4 KEY_ARC BASIC 13 Honolulu San Francisco 75 350 0 500 . 150 11250 . 2 1 KEY_ARC BASIC                   93750

Output 5.2.2: NODEOUT=NODEOUT1

Minimum Cost Flow Problem How to get Hawaiian Pineapples to a London Restaurant Obs _NODE_ _SUPDEM_ _DUAL_ _NNUMB_ _PRED_ _TRAV_ _SCESS_ _ARCID_ _FLOW_ _FBQ_ 1 _ROOT_ 0 0 9 0 1 0 -1 81 -14 2 Atlanta . -136 7 4 8 2 10 150 9 3 Boston . -146 5 3 2 1 5 0 4 4 Chicago . -105 2 1 9 1 1 0 1 5 Heathrow London -500 -212 8 7 5 1 13 150 11 6 Honolulu 500 0 1 9 3 8 -14 0 -1 7 Los Angeles . -79 4 6 7 3 -8 200 3 8 New York . -123 6 3 4 4 7 150 6 9 San Francisco . -75 3 1 6 6 2 150 2